Od stycznia 2014 zadania Ligi Zadaniowej dla Gimnazjów należy wysyłać na adres mejlowy kisowski@gazeta.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Rozwiąż układ równań.
[tex]\left\{ \begin{array}{ll}
x+\frac{12,5}{y}=10 & \\
y+\frac{12,5}{x}=5 & \end{array} \right.[/tex]
Zad. 2. Udowodnij, że liczba 21005+31005 jest podzielna przez 5.
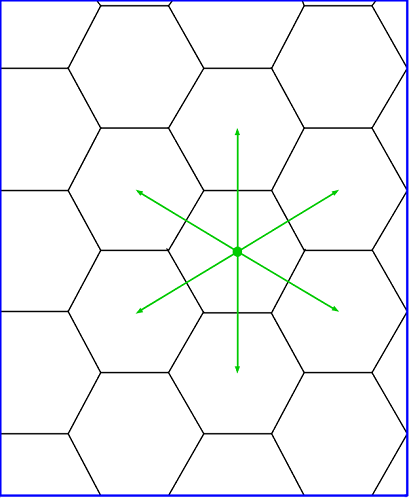
Zad. 3. Mapa heksagonalna jest często używana w grach planszowych. Jest to płaszczyzna szczelnie wypełniona sześciokątami foremnymi (przyjmijmy, że o boku równym 1 cm). Ruch na mapie heksagonalnej polega na przejściu ze środka sześciokąta, w którym się znajdujemy, do jednego z sześciu środków sześciokątów sąsiednich (jak pokazano na rysunku). Przyjmijmy, że ruchy wykonywane są jeden po drugim bez przerw, a każdy z nich zajmuje sekundę. Oblicz prędkości ruchu postępowego na południe i na zachód na tej planszy.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Bartosz Czyżewski GM 1 Jelenia Góra, Joanna Lisiowska KZE Warszawa, Klaudia Marcinkiewicz GM 24 Katowice, Mateusz Rzepecki GM 14 Wrocław, Bartosz Sierpiński GM 3 Brzeg, Michał Stempniak GMSS Ostrów Wielkopolski i Monika Tomaszewska GM 3 Brzeg,
- 2,5 pkt. - Przemysław Rybarczyk GIM Stargard Szczeciński i Wojciech Wiśniewski GM 3 Giżycko,
- 2 pkt. - Maciej Pająk GM 13 Wrocław,
- 1 pkt. - Karolina Stefańczyk GM Radków.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po sześciu miesiącach Ligi z wynikiem 18 pkt. (na 18 możliwych!) prowadzi Bartosz Czyżewski z GM 1 Jelenia Góra. Gratulujemy!
Zad. 1. Z postaci obu równań wynika, że x i y muszą być różne od zera. Zatem możemy równania pomnożyć stronami przez te niewiadome.
[tex]\left\{ \begin{array}{ll}
x+\frac{12,5}{y}=10 & /\cdot y \\
y+\frac{12,5}{x}=5 & /\cdot x\end{array} \right.[/tex]
Otrzymujemy:
[tex]\left\{ \begin{array}{ll}
xy+12,5=10y & \\
xy+12,5=5x &\end{array} \right.[/tex]
Odejmujemy te równania stronami i otrzymujemy:
0=10y-5x
5x=10y
x=2y.
Podstawiamy powyższą zależność do równania xy+12,5=10y:
2y2+12,5=10y
2y2-10y+12,5=0
4y2-20y+25=0
(2y-5)2=0, a to jest zerem wtedy i tylko wtedy, gdy 2y-5=0, czyli y=2,5.
Zatem jedyną parą liczb spełniającą układ równań jest (5, 2.5).
Zad. 2. Aby zbadać podzielność przez 5, wystarczy znaleźć ostatnią cyfrę danej liczby (dlaczego?). Z kolei aby znaleźć ostatnią cyfrę sumy liczb, wystarczy wyznaczyć ostatnie cyfry jej składników (dlaczego?). Wystarczy więc wyznaczyć ostatnie cyfry liczb 21005 i 31005. Ostatnia cyfra potęg dwójki zmienia się cyklicznie co 4 (dlaczego?) i może być jedną z liczb 2, 4, 8, 6. Ostatnia cyfra potęg trójki też zmienia się cyklicznie co 4 (dlaczego?) i może być jedną z liczb 3, 9, 7, 1. Liczba 1005 daje z dzielenia przez 4 resztę 1, zatem ostatnia cyfra liczby 21005 wynosi 2, a liczby 31005 wynosi 3. Stąd liczba 21005+31005 ma ostatnią cyfrę równą 2+3=5. Skoro ostatnia cyfra tej liczby jest równa 5, to liczba jest podzielna przez 5.
Zad. 3. Sześciokąt foremny o boku 1 cm składa się z sześciu trójkątów równobocznych o boku 1 cm. Aby przemieścić się na południe, wystarczy jeden ruch, przy którym pokonuje się odległość równą dwóm wysokościom trójkąta, czyli √3 cm. W celu przemieszczenia się na zachód należy wykonać dwa ruchy, po których oddalimy się w linii prostej na zachód o odległość równą trzem bokom trójkąta, czyli 3 cm. Stąd prędkość ruchu postępowego na południe wynosi √3 cm/s, a na zachód 1,5 cm/s.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
