W grudniowym miniwykładzie mówiliśmy m.in. o histogramie jako o sposobie graficznej prezentacji danych statystycznych. Histogram jest narzędziem bardzo intuicyjnym oraz łatwym w sporządzeniu i w interpretacji (o czym mogli przekonać się ci, którzy zmierzyli się z grudniowymi zadaniami), ale jego poważną wadą jest to, że jego kształt zależy od sposobu wyznaczenia przedziałów, dla których zliczamy obserwacje, a więc zależy on od subiektywnych decyzji osoby, która histogram sporządza. Przygotowanie histogramu w taki sposób, aby można było wyciągnąć z niego interesujące i poprawne wnioski, wymaga więc pewnego kunsztu. Tym razem poznamy narzędzie równie użyteczne, ale całkiem obiektywne, nie wymagające od osoby z niego korzystającej podejmowania decyzji, które mogą zaważyć na interpretacji wyników. Będzie to tzw. wykres pudełkowy (zwany też ramkowym lub wykresem "pudełko-wąsy" ewentualnie "ramka-wąsy" od angielskiego terminu "box and wiskers diagram"). Swoją nazwę zawdzięcza on specyficznemu wyglądowi.
Na początku obejrzymy przykład wykresu pudełkowego, a potem nauczymy się, jak go sporządzić.
Przykład 1. Dla zestawu danych 0,57; 0,64; 0,19; 1,15; 0,3; 0,31; 0,1; 0,52; 0,37; 0,53; 0,44; 0,09; 0,51; 0,67; 0,66; 0,71 wykres pudełkowy wygląda następująco:
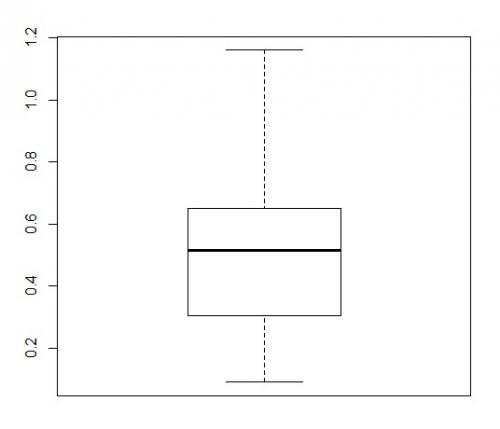
Orientacja wykresu pudełkowego nie ma znaczenia. Może on być położony zarówno pionowo jak i poziomo.
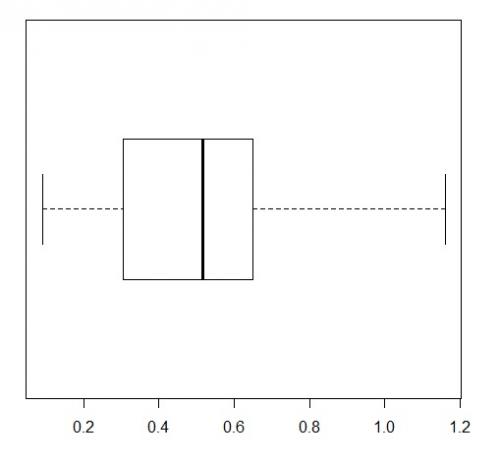
Dla ustalenia uwagi dalej będziemy rysowali wykresu pierwszego typu.
Aby sporządzić wykres pudełkowy, najpierw musimy obliczyć trzech liczb charakteryzujących zestaw danych. Są to (w kolejności rosnącej): pierwszy kwartyl, mediana oraz trzeci kwartyl.
Przykład 2. Wyznaczymy pierwszy kwartyl, medianę i trzeci kwartyl dla danych z przykładu 1. Posłużymy się w tym celu znaną tabelą. Musimy pamiętać, że przed do w tabeli należy mieścić obserwacje po ich uporządkowaniu. Wzory służące do wyznaczenia kwartyli znaleźć można w miniwykładzie ze stycznia.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| pk | 0 | 0,067 | 0,133 | 0,2 | 0,267 | 0,333 | 0,4 | 0,467 | 0,533 | 0,6 | 0,667 | 0,733 | 0,8 | 0,867 | 0,933 | 1 |
| xk | 0,09 | 0,1 | 0,19 | 0,3 | 0,31 | 0,37 | 0,44 | 0,51 | 0,52 | 0,53 | 0,57 | 0,64 | 0,66 | 0,67 | 0,71 | 1,15 |
Pierwszy kwartyl: (0,31-0,3)·((16-1)/4-4+1)+0,3 = 0,3075
Mediana: (0,51+0,52)/2 = 0,515
Trzeci kwartyl: (0,66-0,64)·(3·(16-1)/4-4+1)+0,64 = 0,645
O wykresie pudełkowym mówi się tradycyjnie, że składa się z pudełka i wąsów (patrz: pierwszy rysunek). W środku pudełka narysowano poziomą linię. Oznacza ona medianę (równą w naszym przykładzie 0,515). Dolna krawędź pudełka to pierwszy kwartyl (równy u nas 0,3075) zaś górna to trzeci kwartyl (wynoszący 0,645).
W przypadku wąsów sprawa nie jest już tak prosta. Aby je wyznaczyć, obliczamy rozstęp międzykwartylowy (iq), który - przypomnijmy - jest różnicą między trzecim i pierwszym kwartylem tzn. iq = q3-q1. U nas iq = 0,645 - 0,3075 = 0,3375.
Aby wyznaczyć dolny wąs, wyznaczamy liczbę q1-1,5iq (u nas: 0,3075-1,5·0,3375 = -0,19865). Wówczas dolny wąs jest równy najmniejszej obserwacji niemniejszej od tej liczby.
Dla wyznaczenia górnego wąsa obliczamy q3+1,5iq (u nas: 0,645+1,5·0,3375 = 0,13875). Górny wąs jest równy największej obserwacji niewiększej od tej liczby.
Można więc powiedzieć, że dolny i górny wąs to najmniejsza i największa obserwacja, które zmieściły się w przedziale [q1-1,5iq , q3+1,5iq] (u nas: [-0,19865 , 1,15125]). W naszym przykładzie są to liczby: 0,09 i 1,15.
Obserwacje, które mieszczą się w przedziale [q1-1,5iq , q3+1,5iq], określa się jako tzw. obserwacje odstające (ekstremalnie małe, jeśli sa mniejsze od q1-1,5iq, lub ekstremalnie duże, jeśli są większe od q3+1,5iq). Na wykresie pudełkowym zaznacza się je jako pojedyncze punkty nad i pod wąsami.
Przećwiczmy sporządzanie wykresów pudełkowych dla danych użytych w zadaniach dla gimnazjalistów w etapie grudniowym Ligi.
Przykład 2.
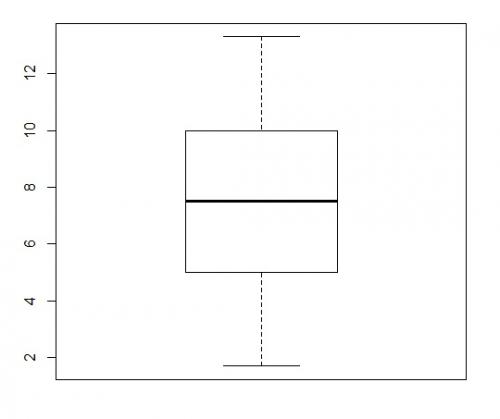
a) Dane: 7,9; 8,7; 3,7; 6,7; 7,1; 1,7; 11,3; 13,3; 6,3; 12,1; 8,3; 9,2; 4,2; 10,8; 2,9; 9,7; 4,7; 5,3; 5,8; 10,3.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pk | 0 | 0,053 | 0,105 | 0,158 | 0,211 | 0,263 | 0,316 | 0,368 | 0,421 | 0,474 |
| xk | 1,7 | 2,9 | 3,7 | 4,2 | 4,7 | 5,3 | 5,8 | 6,3 | 6,7 | 7,1 |
| k | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| pk | 0,526 | 0,579 | 0,632 | 0,684 | 0,737 | 0,789 | 0,842 | 0,895 | 0,947 | 1 |
| xk | 7,9 | 8,3 | 8,7 | 9,2 | 9,7 | 10,3 | 10,8 | 11,3 | 12,1 | 13,3 |
q1= (5,3-4,7)·(19/4-5+1)+4,7 = 5,15; q2 = (7,1+7,9)/2 = 7,5 (q2 oznacza medianę);
q3= (10,3-9,7)·(3·19/4-15+1)+9,7 = 9,85
iq = 9,85-5,15 = 4,7
[q1-1,5iq , q3+1,5iq] = [5,15-1,5·4,7 , 9,85+1,5·4,7] = [-1,9 , 16,9]
dolny wąs: 1,7; górny wąs: 13,3; brak obserwacji odstających
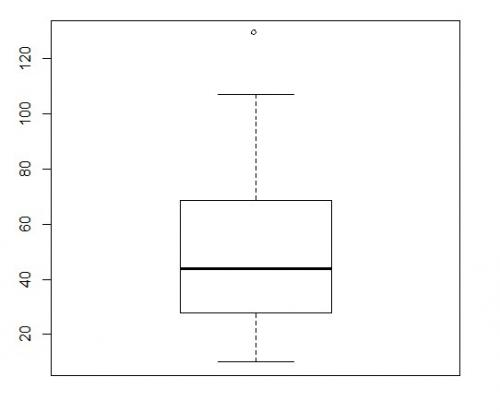
b) Dane: 24; 26; 30; 10; 17; 20; 50; 77; 87; 103; 55; 61; 66; 71; 129; 34; 37; 39; 46; 42.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| pk | 0 | 0,053 | 0,105 | 0,158 | 0,211 | 0,263 | 0,316 | 0,368 | 0,421 | 0,474 |
| xk | 10 | 17 | 20 | 24 | 26 | 30 | 34 | 37 | 39 | 42 |
| k | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| pk | 0,526 | 0,579 | 0,632 | 0,684 | 0,737 | 0,789 | 0,842 | 0,895 | 0,947 | 1 |
| xk | 46 | 50 | 55 | 61 | 66 | 71 | 77 | 87 | 103 | 129 |
q1= (30-26)·(19/4-5+1)+26 = 29; q2 = (42+46)/2 = 44; q3= (71-66)·(3·19/4-15+1)= 67,25
iq = 67,25-29 = 38,25
[q1-1,5iq , q3+1,5iq] = [29-1,5·38,25 , 67,25+1,5·38,25] = [-28,375 , 124,625]
dolny wąs: 10; górny wąs: 103; brak obserwacji odstających ekstremalnie małych;
obserwacja odstająca ekstremalnie duża: 129
Oceniając symetrię danych na podstawie wykresu pudełkowego, możemy powiedzieć, że dane są symetryczne, jeśli mediana wypada w środku pudełka a odległości wąsów od krawędzi pudełka są zbliżone. Dane są lewostronnie asymetryczne, jeśli mediana jest zbliżona do górnej krawędzi pudełka a dolny wąs jest bliżej dolnej krawędzi pudełka niż górny wąs górnej. Z kolei dane są prawostronnie asymetryczne, jeśli warunki te sformułujemy na odwrót.
Przykład 3. Analizując wykresy pudełkowe z wcześniejszego przykładu, możemy wyciągnąć następujące wnioski:
a) Mediana wypada w środku pudełka i jednocześnie wąsy są porównywalnej długości, zatem dane są symetryczne.
b) Mediana jest przesunięta ku dołowi pudełka, a dolny wąs jest wyraźnie krótszy od górnego. Dane są prawostronne asymetryczne.
Warto porównać wykresy pudełkowe histogramami sporządzonymi wcześniej przy okazji rozwiązywania zadań z etapu grudniowego (przykładowe histogramy znajdują się w odpowiedziach do zadań z etapu grudniowego). Warto też porównać wnioski wyciągnięte na podstawie wykresów pudełkowych z wnioskami, jakie wyciągnęliśmy w oparciu o histogramy.
[ koniec wykładu dla gimnazjalistów ]
Wykres pudełkowy pozwala nie tylko zorientować się, czy dane są symetryczne. Daje również rozeznanie, jak dane się rozkładają. Niesie więc bardzo wiele cennych informacji. W szczególności pozwala ocenić, czy w zestawie danych występują obserwacje odstające - ekstremalnie małe lub duże w porównaniu z resztą. W przykładzie 1 występuje jedna obserwacja odstająca, ekstremalnie duża. Występowanie obserwacji odstających utrudnia analizę danych za pomocą wielu procedur statystycznych, dlatego wykrywanie ich obecności jest istotne.
Ktoś mógłby zapytać, dlaczego wybrano akurat kwartyle. Czy nie można było wziąć innych liczb niż 1 i 3? I dlaczego przy wyznaczaniu długości wąsów rozstęp międzykwartylowy jest mnożony akurat przez 1,5? Takie wybory po części mają swoje uzasadnienie w pewnych faktach, które wykraczają poza ramy tego miniwykładu. Niemniej trzeba przyznać, że wybory te są dość umowne. Można sobie wyobrazić sytuację, w której zamiast posługiwać się pierwszym i trzecim kwartylem posługujemy się np. centylami odpowiednich rzędów. Czasem zamiast rozstępu międzykwartylowego rozważa się rozstęp międzydecylowy, który jest różnicą dziewiątego i pierwszego decyla (dziewięćdziesiątego i dziesiątego centyla).
Wykresy pudełkowe pozwalają na łatwe porównanie kilku zestawów danych. W szczególności pozwalają się zorientować, w którym zbiorze danych jest większy rozrzut. Jak już powiedzieliśmy przed miesiącem, rozstęp międzykwartylowy jest (podobnie jak wariancja) miarą rozrzutu danych. Im większe pudełko na wykresie, tym większy rozrzut danych.
Niekiedy na wykresie pudełkowym wąsy oznaczają po prostu obserwację minimalną i maksymalną. Tak sporządzony wykres pudełkowy dostarcza jednak mniej informacji, stąd powyżej przedstawiliśmy bardziej skomplikowaną konstrukcję, jednak pozwalającą uzyskać więcej informacji o danych.
Zad. 1. (2 punkty) Sporządź wykresy pudełkowe dla następujących zestawów danych:
a) 25; 18; 17; 21; 23; 19; 26; 18; 17; 18; 21; 23; 20; 18; 20; 23; 18; 16; 18; 20; 25; 18; 21; 21; 21;
b) 6,0; 32,4; 6,0; 48,2; 28,8; 0,6; 26,7; 23,4; 13,1; 7,9; 7,8; 0,8; 13,2; 7,0; 2,5; 0,8; 53,8; 2,8; 61,8; 12,4; 5,3; 0,6; 3,2; 3,3; 2,3.
Na podstawie wykresów pudełkowych oceń symetrię tych danych.
W rozwiązaniu nie musisz przesyłać rysunków. Wystarczy, że dla każdego zestawu danych wypiszesz: obserwacje odstające ekstremalnie małe, dolny wąs, pierwszy kwartyl, medianę, trzeci kwartyl, górny wąs i obserwacje odstające ekstremalnie duże.
Zad. 2. (1 punkt) Wyobraźmy sobie, że sporządziliśmy wykres pudełkowy na podstawie zestawu danych x1, x2, ..., xn. Następnie wszystkie dane przekształcamy za pomocą funkcji o wzorze f(x)=ax+b, gdzie a≠0. Innymi słowy bierzemy nowy zestaw danych: y1 = ax1+b, y2 = ax2+b, ..., yn = axn+b. Jak po takim przekształceniu zmieni się wykres pudełkowy?
Zad. 1. (2 punkty) Wykonaj zadanie 1 dla gimnazjalistów.
Zad. 2. (1 punkt) Wyobraźmy sobie, że sporządziliśmy wykres pudełkowy na podstawie zestawu danych x1, x2, ..., xn, przy czym zakładamy, że wszystkie obserwacje są nieujemne oraz że wykres pudełkowy sporządzony na podstawie tego zbioru danych jest idealnie symetryczny tzn. mediana wypada dokładnie w środku odległości między pierwszym i trzecim kwartylem a oba wąsy są tej samej długości. Następnie oryginalne dane zastępujemy przez dane spierwiastkowane tzn. naszymi nowymi obserwacjami będą liczby [tex]sqrt{x_1}, sqrt{x_2}, \dots, sqrt{x_n}[/tex]. Jakie po takim przekształceniu będzie położenie nowej mediany względem nowego pierwszego i nowego trzeciego kwartyla? Jak będą się miały do siebie długości nowych wąsów?
Wskazówka: Pierwiastek kwadratowy spełnia następujące twierdzenie:
Jeśli 0≤ w ≤ x ≤ y ≤ z i x-w = z-y, to [tex]\sqrt{x}-\sqrt{w} \geq \sqrt{z}-\sqrt{y}[/tex].
Za rozwiązanie zadań z etapu lutowego Joanna Lisiowska zdobyła 2,5 punktu a pozostali uczestnicy, którzy nadesłali rozwiązania, uzyskali 1,5 punktu.
Tym samym czołówka klasyfikacji generalnej przybrała następujący kształt: Joanna Lisiowska (I miejsce), Aleksandra Domagała (II miejsce) i Mieszko Baszczak (III miejsce).
Lutowy etap Ligi z Analizy przyniósł następujące zdobycze punktowe:
- Tomasz Stempniak - 2,5 punktu,
- Daria Bumażnik - 1,5 punktu,
- Krzysztof Danielak - 1 punkt.
Czołówka klasyfikacji pozostaje bez zmian; nadal na prowadzeniu Tomasz Stępniak, dalej
Daria Bumażnik (II miejsce) i Krzysztof Danielak (III miejsce).
Zad. 1. Oba zestawy danych liczą po 25 elementów. Łatwo widać, że po uporządkowaniu obserwacji od najmniejszej do największej pierwszy kwantyl będzie równy siódmej obserwacji, mediana - trzynastej obserwacji a trzeci kwartyl - dziewiętnastej obserwacji z kolei.
a) min = 16; q1 = 18; q2 = 20; q3 = 21; max = 26
iq = 21 - 18 = 3
[q1 - 1,5iq ; q3 + 1,5iq] = [18 - 1,5 · 3 ; 21 + 1,5 · 3 ] = [18 - 4,5 ; 21 + 4,5] = [13,5 ; 25,5]
Wykres pudełkowy:
- obserwacje odstające ekstremalnie małe: brak
- dolny wąs: 16
- pierwszy kwartyl: 18
- mediana: 20
- trzeci kwartyl: 21
- górny wąs: 25
- obserwacje odstające ekstremalnie duża: 26
b) min = 0,6; q1 = 2,8; q2 = 7; q3 = 23,4; max = 61,8
iq = 23,4 - 2,8 = 20,6
[q1 - 1,5iq ; q3 + 1,5iq] = [2,8- 1,5 · 20,6 ; 23,4 + 1,5 · 20,6 ] = [2,8 - 30,9 ; 23,4 + 30,9 ] = [-28,1 ; 54,3]
Wykres pudełkowy:
- obserwacje odstające ekstremalnie małe: brak
- dolny wąs: 0,6
- pierwszy kwartyl: 2,8
- mediana: 7
- trzeci kwartyl: 23,4
- górny wąs: 53,8
- obserwacje odstające ekstremalnie duża: 61,8
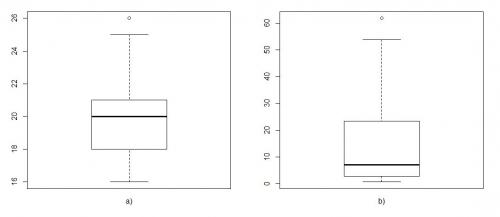
W ocenie symetrii rozkładu na podstawie wykresu pudełkowego bardzo pomaga narysowanie tego wykresu, natomiast analiza poszczególnych liczb, jakie sa na nim zaznaczone, bez wizualizacji może okazać się niewystarczająca.
Ocena symetrii w przypadku zestawu danych a) nastręcza pewnych trudności. Z jednej strony mediana wypada bliżej górnej grawędzi pudełka niż dolnej, ale z drugiej strony górny wąs jest dłuższy niż dolny oraz pojawia się obserwacja odstająca ekstremalnie duża. W odczuciu autora zadania o tym zestawie danych można powiedzieć, że są prawostronnie asymetryczne, przy czym asymetria nie jest znaczna, więc ostrożne zaklasyfikowanie tych danych jako symetrycznych też uznaje się za poprawne. Natomiast nie można powiedzieć, że dane te są lewostronnie asymetryczne, co jest dobrze widoczne na rysunku.
Dane z zestawu b) są prawostronnie asymetryczne.
Zad. 2. Wszystkie obiekty na wykresie pudełkowym zostają przekształcone przez funkcję f(x) = ax + b.
Jeśli a > 0, to obserwacje odstające ekstremalnie małe pozostaną obserwacjami odstającymi eksptremalnie małymi, dolny wąs przejdzie na dolny wąs, dolna krawędź pudełka na dolną krawędź pudełka, mediana na medianę, górna krawędź pudełka na górną krawędź pudełka, górny wąs na górny wąs a obserwacje odstające ekstremalnie duże pozostaną obserwacjami odstającymi eksptremalnie dużym.
Jeśli a < 0, to obserwacje odstające ekstremalnie małe staną się obserwacjami odstającymi eksptremalnie dużymi, dolny wąs
przejdzie na górny wąs (i na odwrót), dolna krawędź pudełka na górną krawędź pudełka (i na odwrót). Mediana przejdzie na medianę.
Można więc powiedzieć, że kształ wykresu pudełkowego sporządzonego na podstawie danych przekształconych w opisany sposób nie zmieni kształtu. Zmieni się jego rozmiar (po przekształceniu wszystkie odległości zostaną pomnożone przez |a|), a dodatkowo jeśli a < 0, to wykres zostanie odwrócony "do góry nogami".
Zad. 1. Odpowiedź jak w zadaniu 1 dla gimnazjalistów.
Zad. 2. Wszystkie obiekty występujące na wykresie pudełkowym zostaną przekształcone na analogiczne obiekty na drugim wykresie.
Jeśli oznaczymy dolny wąs na wyjściowym wykresie pudełkowym jako w1, górny wąs jako w2, pierwszy kwartyl jako q1, trzeci kwartyl jako q3 i medianę jako q2, to możemy powiedzieć, że na wykresie po przekształceniu dolny wąs będzie wypadał w punkcie [tex]\sqrt{w_1}[/tex], pierwszy kwartyl w punkcie [tex]\sqrt{q_1}[/tex], mediana w punkcie [tex]\sqrt{q_2}[/tex], trzeci kwartyl w punkcie [tex]\sqrt{q_3}[/tex] a górny wąs będzie wypadał w punkcie [tex]\sqrt{w_2}[/tex].
Wiemy, że q2 - q1 = q3 - q2. Wobec tego [tex]\sqrt{q_2}-\sqrt{q_1} \geq \sqrt{q_3}-\sqrt{q_2}[/tex], czyli odległość od pierwszego kwartyla do mediany po przekształceniu jest większa niż odległość od trzeciego kwartyla do mediany.
Podobnie wiemy, że q1 - w1 = w2 - q3. Wobec tego [tex]\sqrt{q_1}-\sqrt{w_1} \geq \sqrt{w_2}-\sqrt{q_3}[/tex],
czyli odległość od pierwszego kwartyla do mediany po przekształceniu
jest większa niż odległość od trzeciego kwartyla do mediany.
Z tego wynika, że po spierwiastkowaniu dane z symetrycznych stały się prawostronnie asymetryczne.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
