Zadanie 1. Przez wierzchołki A i B trójkąta ABC przechodzi okrąg o promieniu r i przecina bok BC w punkcie D. Znajdź promień okręgu opisanego na trójkącie ADC, wiedząc że AB=c oraz AC=b.
Zadanie 2. Wykaż, że prawdziwy jest wzór: 1/ab + 1/bc + 1/ac = 1/2Rr, gdzie a, b, c są długościami boków trójkąta, a R i r promieniami okręgów opisanego na tym trójkącie i wpisanego w ten trójkąt.
Zadanie 3. Pięciokąt ABCDE wpisano w okrąg. Punkty M, N, P i Q są rzutami prostokątnymi wierzchołka E odpowiednio na proste AB, BC, CD i przekątną AD. Oblicz długość EM, wiedząc że EN=d oraz stosunek pól trójkątów MQE i PNE wynosi k.
Zadanie 4. (wolna amerykanka) W trójkącie równoramiennym AB=BC. Niech D będzie środkiem boku AC. Niech K będzie punktem na boku BC takim, że prosta DK jest prostopadła do BC. Niech M będzie środkiem odcinka DK. Wykaż, że proste AK i BM są prostopadłe.
Ze względu na pojawienie się błędu w treści zadania 3 nie będzie ono wliczane do punktacji. Przepraszamy za powstałe zamieszanie.
W lutym 20 pkt. uzyskali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Anna Gudełajtis (uczennica, II LO Opole), Michel Migas (student, PW), Krzysztof Sobków (nauczyciel, II LO Opole), Sabina Sy (studentka nanotechnologii, UJ), Iwona Gruszecka (nauczycielka, G 28 Wrocław), Agmieszka Borucka (uczennica, II LO Opole).
Za zadanie "wolna amerykanka 10 pkt. zdobyli: Jacek Bagiński, Włodzimierz Bąk, Michel Migas, Krzysztof Sobków oraz Tadeusz Porzucek (emeryt, Gostyń)
Tuż za półmetkiem Ligi punktacja w czołówce wygląda następująco:
- zadania 1 - 3
Jacek Bagiński 140 pkt, Włodzimierz Bąk 140 pkt, Michel Migas 138 pkt, Krzysztof Sobków 136 pkt, Iwona Gruszecka 136 pkt, Anna Gudełajtis 120 pkt, Tadeusz Porzucek 114 pkt, Sabina Sy 110 pkt, Agnieszka Borucka 104 pkt. - wolna amerykanka
Jacek Bagiński 50 pkt, Włodzimierz Bąk 50 pkt, Michel Migas 50 pkt, Krzysztof Sobków 50 pkt, Tadeusz Porzucek 50 pkt, Sabina Sy 38 pkt, Daria Bumażnik (uczennica, II LO Jelenia Góra) 30 pkt, Arkadiusz Wróbel (student, PW) 30 pkt.
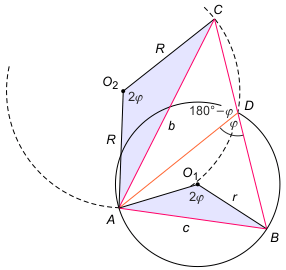
Zadanie 1. Niech |∡ADB| = φ. Wówczas |∡ADC| = 180° - φ. Dalej kąt środkowy wklęsły CO2A ma miarę 360° - 2φ, stąd kąt CO2A w trójkącie AO2C ma miarę 2φ . Z drugiej strony |AO1B| = 2φ. Oznacza to, że trójkąty równoramienne AO1B i AO2C są podobne. Otrzymujemy R/b = r/c. Stąd R = br/c. Podobieństwo wskazanych trójkątów zachodzi także gdy φ ≥ 90°.
Zadanie 2. Zauważmy, że 1/ab + 1/bc + 1/ac = c/abc + a/abc + b/abc = (a+b+c)/abc = 2p/abc = (2S/r )/4RS = 1/2Rr, gdzie S oznacza pole trójkąta i stosujemy wzory S = pr oraz S = abc/4R.
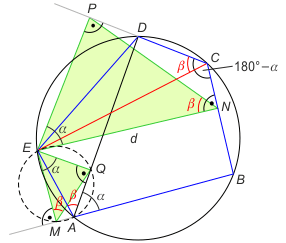
Zadanie 3. Niech |∡DAB| = α. Wówczas |∡MEQ| = α (bo na czworokącie MAQE można opisać okrąg - przeciwległe kąty są proste, a |∡MAQ| = 180° - α. Z drugiej strony |∡DCB| = 180° - α (bo czworokąt ABCD jest wpisany w okrąg). Stąd |∡PEN| = α (z sumy kątów w czworokącie ENCP). Niech |∡PCE| = β. Wówczas |∡PNE| = β (bo na czworokącie ENCP można opisać okrąg) oraz |∡EBD| = β (oparty na łuku ED). Dalej |∡EMQ| = β (oparty na łuku EQ). Oznacza to, że trójkąty EMQ i EPN są podobne w skali √k. Stąd otrzymujemy EM = d√k.
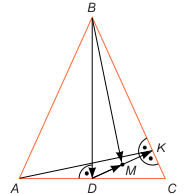
Zadanie 4. Wystarczy wykazać, że iloczyn skalarny wektorów BM i AK jest równy 0. Zauważmy że BM•AK = (BD+DM)•(AC+CK) = BD•AC + BD•CK + DM•AC + DM•CK = 0 + BD•CK + DM•AC + 0 = DM•2DC + BD•(CD+DK) = 2DM•DC + BD•CD + BD•DK = 2DM•DC + 0 + BD•DK = DK•(BD+DC) = DK•BC = 0.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
