Zad. 1. W trójkącie ABC kąt B jest prosty. Na boku AB obrano punkt O, który jest środkiem okręgu o promieniu r= OB, stycznego do boku AC w punkcie D, a na boku BC obrano taki punkt E, że |BE|=4. Wiedząc, że |AC|=15 i |AB|=12, znajdź miarę kąta, pod jakim przecinają się odcinki BD i AE.
Zad. 2. Proste wyznaczone przez dwusieczne kątów A, B i C trójkąta ABC przecinają okrąg opisany na tym trójkącie w punktach odpowiednio K, L i M. Wykaż, że |AK|+|BL|+|CM| > |AB|+|BC|+|AC|.
Zad. 3. W trójkącie ostrokątnym ABC niech H1, H2 i H3 są spodkami wysokości opuszczonych odpowiednio z wierzchołków A, B i C. Na odcinkach H1H3 i H2H3 obrano odpowiednio punkty M i N tak, że |∡MAH1| = |∡NAC|. Wykaż, że MA jest dwusieczną kąta H3MN.
Zad. 4. (wolna amerykanka) Dany jest kwadrat ABCD. Punkt M jest środkiem boku AB. Na boku AD obrano punkt K taki, że |DK|=|KM|, a na boku BC obrano punkty E i F takie, że KE jest dwusieczną kąta DKM oraz kąt KMF jest prosty. Wiedząc, że |EF|=5, oblicz pole kwadratu ABCD.
W tym miesiącu za zadania 1-3
punkty otrzymali:
- 30 - Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Mikołaj Popek (student UAM) oraz Tadeusz Porzucek (emerytowany nauczyciel z Gostynia),
- 20 - Elżbieta Grzechnik (emerytowana nauczycielka z Radomia) i Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Z twierdzenia Pitagorasa otrzymujemy |BC|=9 i dalej |EC|=5. Zauważmy, że |CE|:|EB| = 5/4 = |AC|:|AB|, co oznacza, że AE jest dwusieczną kąta A. W trójkącie równoramiennym DBC mamy |∡DBC|= 90°–γ/2, skąd |∡ABD|=γ/2. Ostatecznie szukany kąt EKB jest zewnętrzny dla trójkąta ABK, a jego miara jest sumą α/2+γ/2 = 45°.
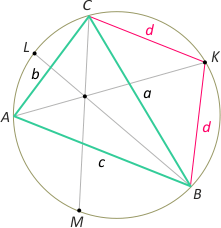
Zad. 2. Rozważmy czworokąt ABKC i zastosujmy do niego twierdzenie Ptolomeusza: (*) |AK|·a = d·(b+c). Z nierówności trójkąta mamy 2d > a, skąd d/a > 1/2. Podstawiając to do (*), otrzymujemy |AK| = (d/a)·(b+c) > (b+c)/2. Analogicznie mamy |BL| > (a+c)/2 i |CM| > (a+b)/2. Dodając te nierówności stronami, otrzymujemy tezę.
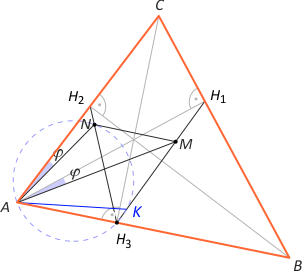
Zad. 3. Zauważmy, że |∡MAN| = φ+|∡NAH1| = φ+((90°–γ)–φ)) = 90°–γ. Niech prosta AK będzie symetryczna do AN względem prostej AM. Wówczas |∡NAK| = 180°–2γ = |∡NH3M| (z własności trójkąta spodkowego - patrz zad. 2. z października 2014). Oznacza to, że punkty A, H3, K i N są współokręgowe. Na cięciwie AN oparty jest kąt γ, a na cięciwie AK oparty jest kąt ANK o mierze180°–γ. Zauważmy, że |∡ANK| + |∡AH3N| = 180°, z czego wynika równość długości cięciw AK i AN. Oznacza to przystawanie trójkątów ANM i AKM, skąd wynika teza.
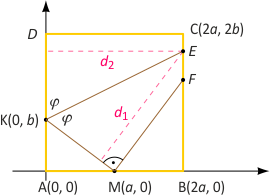
Zad. 4. (wolna amerykanka) Umieśćmy kwadrat w układzie współrzędnych jak na rysunku. Z twierdzenia Pitagorasa dla trójkąta AMK otrzymujemy b=(3/4)a. Niech punkt F ma współrzędne (2a, c). Wówczas MKºMF = (-a, 3a/4)º(a, c) = 0, czyli -a2+3ac/4 = 0, skąd c=4a/3. Zatem F=(2a, 4a/3). Dalej E=(2a, 5+4a/3). Punkt E leży na dwusiecznej kąta DKM, zatem równe są odległości d1 i d2. Równanie prostej KM ma postać 3x+4y–3a = 0, skąd d1 = 4+5a/3. Ostatecznie rozwiązaniem równania d1 = d2 jest a=12. Zatem |AB|=24 i szukane pole kwadratu wynosi 576.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
