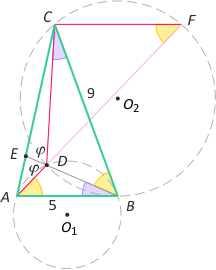
Zad. 1. Przez wierzchołki A i B trójkąta ABC przechodzi okrąg styczny do prostej BC, a przez wierzchołki B i C - drugi okrąg styczny do prostej AB. Przedłużenie wspólnej cięciwy BD obu okręgów przecina bok AC w punkcie E, a prosta AD przecina drugi okrąg w punkcie F. Wiedząc, że |AB|=5 i |BC|=9, oblicz |AE|:|EC| oraz porównaj pola trójkątów ABC i ABF.
Zad. 2. W trójkącie równobocznym ABC na boku AB obrano punkty E i F takie, że |AE|=2, |FB|=3 i |∡ECF|=30°. Oblicz długość EF.
Zad. 3. W trójkącie ABC odcinki AD i BE są wysokościami, a M jest środkiem boku AB. Wiedząc, że |ED|=|DM|, znajdź miarę kąta C.
Zad. 4. (wolna amerykanka). W trójkącie ABC o boku |AC|= 8 poprowadzono dwusieczną BL. Wiedząc, że stosunek pól trójkątów ABL i BLC wynosi 3:1, oblicz długość odcinka dwusiecznej BL zawartego w trójkącie, przy której wysokość BH jest najdłuższa.
W tym miesiącu za zadania 1-3 punkty po 30 pkt. otrzymali: Dominik Bysiewicz (student matematyki na UJ), Robert Ciężabka (korepetytor, Osiek Jasielski), Radosław Górzyński (uczeń I LO Lubin), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) oraz Marzena Wąsiewicz (nauczycielka z Kajetan).
Za zadanie 4 po 10 pkt. otrzymali: Dominik Bysiewicz, Robert Ciężabka, Radosław Górzyński, Elżbieta Grzechnik, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek oraz Marzena Wąsiewicz. Gratulacje!
Zad. 1. Zauważmy, że kąty dopisane DBC i ABE są przystające odpowiednio do kątów DAB i DCB, skąd wynika podobieństwo trójkątów ABD i BCD w skali k = |AB|:|BC| = 5/9. Mamy zatem |AD|:|DB| = 5/9 oraz |DB|:|CD| = 5/9. Mnożąc te równości stronami, otrzymujemy |AD|:|CD| = 25/81. Dalej zauważamy, że kąty zewnętrzne CDE i ADE są przystające, skąd wynika, że ED jest dwusieczną kąta ADC i na mocy twierdzenia o dwusiecznej kąta wewnętrznego mamy |AE|:|EC| = |AD|:|CD| = 25/81. Dalej mamy oczywistą równość miar kątów wpisanych CFD i DBC, z której wynika równoległość prostych CF i AB, bo przystające są kąty naprzemianległe AFC oraz FAB. Oznacza to, że pola trójkątów ABC i ABF są równe.
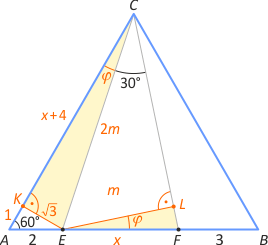
Zad. 2. Niech K i L będą rzutami prostokątnymi punktu E odpowiednio na odcinki AC i FC. Zauważmy, że otrzymujemy dwa trójkąty ekierkowe AEK oraz ELC, w których zachodzi |EK|=√3, |EL|=m i |EC|=2m. Zauważmy teraz, że kąt zewnętrzny CEF trójkąta AEC ma miarę 60°+|∡ACE|, a stąd mamy równość miar kątów ACE i LEF. Oznacza to, że trójkąty ACE i EFL są podobne. Mamy zatem proporcję m:x = (x+4):2m, skąd 2m2 = x2+4x. Z kolei z twierdzenia Pitagorasa dla trójkąta KEC mamy 4m2 = 3+(x+4)2. Ostatecznie 2x2+8x = 3+(x+4)2, skąd x = √19.
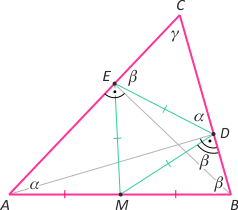
Zad. 3. Zauważmy, że z własności środkowej przeciwprostokątnej w trójkątach ABD i ABE mamy |DM|=|EM|= |AB|/2, co oznacza, że trójkąt MDE jest równoboczny, a trójkąt MBD - równoramienny przy czym |∡MDB|=β. Z własności trójkąta spodkowego (patrz zad. 2. październik 2014) mamy |<EDC|=α. Łatwo zauważyć, że α+β = 180°–|∡MDE| = 180°–60° = 120°. Zatem szukany kąt C ma miarę 60°.
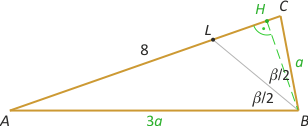
Zad. 4. (wolna amerykanka) Zachodzi SABL:SBLC = 3/1 = |AL|:|LC| = |AB|:|BC|, skąd |AB| = 3·|BC|. Ze wzoru Herona mamy SABC = 2(√((16–a2)·(a2–4)). Z drugiej strony SABC = |AC|·|BH|/2 = 4·|BH|. Otrzymujemy 4·|BH| = 2(√((16–a2)·(a2–4)) ≤ 16–a2+a2–4 = 12 (nierówność Cauchy'ego), skąd |BH|≤3, przy czym równość zachodzi dla 16–a2 = a2–4, czyli dla a = √10. Mamy wówczas |BC|=√10 i |AB|=3√10. Rozważmy teraz trójkąt ABH, w którym sinA = |BH|:|AB| = 3/(3√10) = 1/√10, cosA = 3/√10. Z twierdzenia o dwusiecznej kata mamy |AL| = 3·|LC|, skąd |AL|:|AC| = 3/4. Mamy |AL| = |AC|·(|AL|/|AC|) = 8·(3/4) = 6. Ostatecznie z twierdzenia kosinusów w trójkącie ABL mamy |BL| = 3√2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
