Zad. 1. W trójkącie ABC dwusieczna kąta A przecina bok BC w punkcie D. Wiadomo, że |AB|–|BD| = a oraz |AC| + |CD| = b. Oblicz długość AD.
Zad. 2. W trójkącie prostokątnym ABC przeciwprostokątna AB ma długość c. Na wysokości CD jako na średnicy zbudowano okrąg. Proste, które przechodzą przez punkty A i B oraz są styczne do okręgu odpowiednio w punktach M i N, przecinają się w punkcie K. Oblicz długość MK.
Zad. 3. Niech H oznacza ortocentrum (czyli punkt przecięcia prostych zawierających wysokości) trójkąta ABC, w którym |AB| ≠ |AC|. Niech M i N będą środkami odpowiednio odcinków BC i AH, a K będzie punktem przecięcia prostej MN z dwusieczną kąta A. Wykaż, że kąt AKH jest prosty.
Zad. 4. (wolna amerykanka) Na trójkącie prostokątnym opisano okrąg. Drugi okrąg o takim samym promieniu jest styczny do przyprostokątnych tego trójkąta, przy czym jednym z punktów styczności jest wierzchołek trójkąta. Oblicz stosunek pola trójkąta do pola części wspólnej kół ograniczonych oboma danymi okręgami.
Uwaga! Zapraszamy wszystkich chętnych do rejestracji na XVIII Mistrzostwa Polski w Geometrii Elementarnej. Zawody odbędą się w trybie zdalnym 16 V. Formularz rejestracyjny jest dostępny tutaj.
Za zadania 1-3 punkty otrzymali:
30 pkt - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Łukasz Besuch (III LO Wrocław), Dominik Bysiewicz (I LO Krosno), Krzysztof Lis (XIV LO Warszawa), Michel Migas (student PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń);
10 pkt. - Jerzy Kawka (ILO Kraków)
Za zad. 4 punkty otrzymali:
10 pkt. - Michel Migas, Dominik Bysiewicz, Krzysztof Lis, Jacek Bagiński, Zygmunt Krawczyk (nauczyciel SLO Żary) oraz Łukasz Besuch;
8 pkt. - Tadeusz Porzucek.
Gratulujemy!
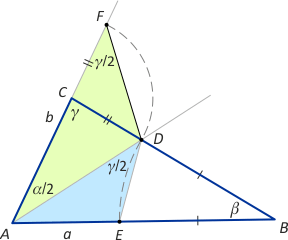
Zad. 1. Zauważmy, że kąt C o mierze γ jest kątem zewnętrznym trójkąta CDF, stąd |∡CFD| = γ/2. W trójkącie ADF mamy więc |∡ADF| = 90°+ β/2. Z drugiej strony |∡AED| = 180°–|∡DEB| = 180°–1/2(180°–β) = 90°+ β/2. Oznacza to, że trójkąty AED i ADF są podobne, skąd mamy proporcję |AD|:|AF| = |AE|:|AD|, a stąd |AD|2 = |AF|·|AE| = a·b i ostatecznie |AD| = √(ab).
Zad. 2. Niech |CD| = 2r. Wówczas 4r2 = d·(c–d), skąd r = 1/2√(d(c–d)). Obliczając pole trójkąta ABK ze wzoru Herona, otrzymujemy PABK = √((x+c)(c–d)dx). Z drugiej strony, obliczając pole z wykorzystaniem promienia okręgu wpisanego w trójkąt mamy PABK = (x+c)·1/2√(d(c–d). Po przekształceniach otrzymujemy x = c/3.

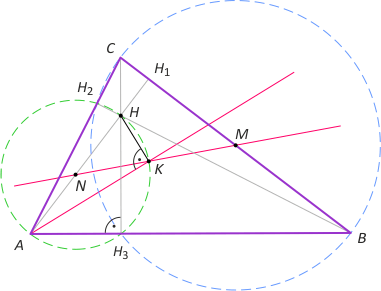
Zad. 3. Zauważmy, że czwórki punktów A, H3, H, H2 oraz H3, B, C, H2 są współokręgowe (leżą odpowiednio na okręgach s1 i s2 o środkach odpowiednio N i M). Oznacza to, że prosta MN jest symetralną odcinka H2H3 i przecina okrąg s1 w tym samym punkcie K co dwusieczna kąta A. Zatem kąt AKH jest wpisany w s1 i oparty na średnicy AH, a stąd wynika teza.
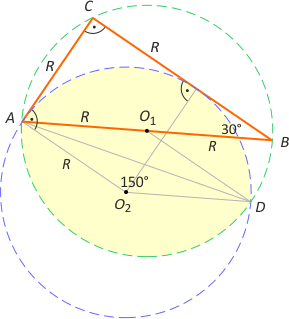
Zad. 4. (wolna amerykanka) Zauważmy, że czworokąt AO2EC jest kwadratem o boku R. W trójkącie ABC przyprostokątna jest dwa razy krótsza od przeciwprostokątnej, więc kąt ABC ma miarę 30°. Oznacza to, że kąt O1AO2 ma miarę 30°, a kąt DAO2 ma 15°, skąd w trójkącie równoramiennym AO2D kąt środkowy AO2D ma miarę 150°. Część wspólna obu kół jest sumą dwóch takich samych odcinków koła (odcinek koła jest róznicą odpowiedniego wycinka koła i trójkąta). Pole części wspólnej wynosi P = 2·(5/12πR2 – 1/2R2sin150°) = 1/2R2(5π/3– 1). Natomiast PABC = √3/2R2. Ostatecznie szukany stosunek pól wynosi 3√3 : (5π–3).