Zad. 1. Udowodnij, że dla dodatniego nieskracalnego ułamka x/y mniejszego od 1, ułamek dopełniający go do jedynki jest również nieskracalny.
Zad. 2. Wyznacz wszystkie liczby naturalne n, dla których 14n-9 jest liczbą pierwszą.
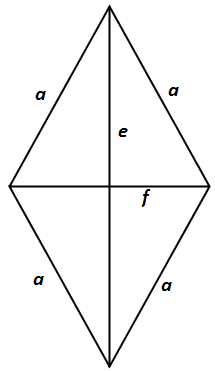
Zad. 3. Dla jakiego kąta ostrego w rombie długość boku rombu jest równa średniej geometrycznej długości jego przekątnych?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kamila Bojar ZSP Szprotawa, Konrad Budzyński IX LO Wrocław, Bartosz Czyżewski I LO Jelenia Góra, Dawid Hanrahan I LO Brzeg, Piotr Jażdżewski I LO Oleśnica, Szymon Meyer II LO Opole, Piotr Paduszyński SLO Żary, Tomasz Stempniak I LO Ostrów Wielkopolski i Wojciech Wiśniewski I LO Giżycko;
- 2,5 pkt. - Robert Czwartosz LO Trzebnica i Mateusz Grzeliński II LO Lubin;
- 2 pkt. - Piotr Pojda ZSO Głubczyce;
- 1 pkt. - Krzysztof Bednarek III LO Wrocław;
- 0,5 pkt. - Cyprian Skóra LO Głubczyce i Marta Włóczyk OSSP Opole.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Po sześciu miesiącach Ligi Zadaniowej z wynikiem 18 pkt. (na 18 możliwych) prowadzi: Bartosz Czyżewski. Drugie miejsce z wynikiem 17,5 pkt. zajmują: Konrad Budzyński, Piotr Paduszyński i Tomasz Stempniak. Trzecie miejsce z wynikiem 17 pkt. zajmuje Szymon Meyer.
Gratulujemy!
Zad. 1. Załóżmy nie wprost, że ułamek dopełniający x/y do jedynki jest skracalny, czyli że y-x/y = n·a/n·b, gdzie n, a i b są liczbami naturalnymi i NWD(a, b) = 1 oraz b>a. Stąd y = n·b oraz x = n·(b-a), czyli ułamek x/y = b-a/b jest skracalny, co jest sprzeczne z założeniem, a to kończy dowód.
Zad. 2. Tylko dla n=1 dostajemy liczbę pierwszą równą 5. Dla parzystych n=2k, k = 1, 2, ... dostajemy liczbę złożoną 142k-9 = (14k+3)·(14k-3). Dla nieparzystych n=2k+1, k = 1, 2, ... liczba 142k+1 kończy się cyfrą 4, więc po odjęciu 9 ostatnią cyfrą liczby 142k+1-9 jest 5, zatem jest to liczba złożona.
Zad. 3. Dla rombu zachodzi własność a = (e·f)0,5. Pole rombu możemy obliczyć na dwa sposoby: P = e·f/2 = a2·sinβ, gdzie β jest kątem ostrym rombu. Stąd łatwo zauważyć, że sinβ=1/2, czyli β=30o.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
