Zad. 1. Pokaż, że jeśli a/b = b/c, to [tex]\frac{a^2+b^2}{b^2+c^2}=\frac{a}{c}[/tex].
Zad. 2. Trzy ekipy budowlane zaoferowały swoje usługi panu Kowalskiemu, który chce wyremontować mieszkanie. Pierwszej ekipie remont zajmie 12 dni, drugiej 15 dni, a trzeciej tylko 8 dni. Ile dni zająłby remont mieszkania Kowalskiego gdyby wszystkie ekipy pracowały razem?
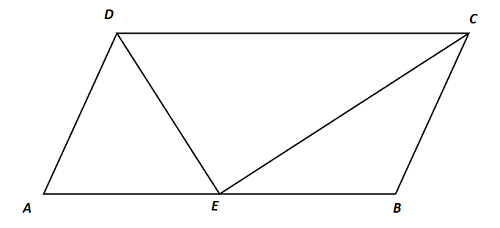
Zad. 3. W równoległoboku ABCD zachodzi |AB|=2|BC|. Punkt E dzielący bok AB na połowy połączono z wierzchołkami C i D. Oblicz miarę kąta CED.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Mieszko Baszczak - SP 301 Warszawa, Antoni Buraczewski - SP 107 Wrocław, Hubert
Cymbalista - SP 1 Sobótka, Michał Gębarowski - SP Polna, Szymon Grech - NSP Koszarawa Bystra, Natasza Henko - SP Mieroszów, Igor Hołowacz - SP Bielany Wrocławskie, Antoni Kołat - SP 45 Wrocław, Marek Komorowski - SP 5 Żory, Martyna Kubiak - SP Skoki, Szymon Kubiak - SP Skoki, Kacper Kuszaj - SP 2 Jelcz-Laskowice, Weronika Mucha - SP 5 Ozorków, Gabriela Poświata - SSP 35 Legionowo, Jakub Ptak - SP 64 Wrocław, Mikołaj Roszczyk - SP 7 Legionowo, Kaja Srokosz - SP 52 Warszawa, Adam Stachelek - SP 301 Warszawa, Bartosz Szczerba - SP 35 Szczecin, Michalina Więckowska - SP 1 Konstancin-Jeziorna i Aleksandra Zalewska - SP 1 Sokółka; - 2,5 pkt. - Konrad Andruchów - SP 4 Bolesławiec, Hubert Grześkowiak - SP Mieroszów, Natasza Ptak - SP 118 Wrocław i Klaudia Sułkowska - SP Mieroszów;
- 2 pkt. - Kacper Bernaciak - SP 30 Wrocław, Mikołaj Bilski - SP 6 Jelenia Góra, Antoni Bryszewski - SP 15 Jelenia Góra, Lena Bukowska - SP 1 Sobótka, Gracjan Ciupa - SP 72 Wrocław, Norbert Frydrysiak - SP Mszczonów, Joachim Górski - SP Mszczonów, Karolina Kamińska - OSM Wrocław, Gabriela Kelner - SP Mieroszów, Kajetan Pacześniak - SP 46 Wrocław, Szymon Warmuła - SP Kobierzyce i Jerzy Wąsiewicz - SP Kostowiec;
- 1,5 pkt. - Janina Popławska - SP 4 Legnica;
- 1 pkt. - Jakub Badowski - SP Mszczonów, Łukasz Banaś - SP 46 Wrocław, Malwina Górecka
- SP 11 Inowrocław i Kacper Tylek - SP Świątniki Górne; - 0,5 pkt. - Karol Raczkowski-Orleski - SP 45 Wrocław.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Po sześciu miesiącach Ligi Zadaniowej dla SP prowadzą: Gratulujemy!
Zad. 1. Zauważmy, że z równości a/b = b/c wynika, że b≠0, c≠0 i a≠-c, dlatego wyrażenie [tex]\frac{a^2+b^2}{b^2+c^2}=\frac{a}{c}[/tex] jest dobrze określone. Warunek a/b = b/c jest równoważny b2=a·c. Podstawiając za b2, dostaniemy [tex]\frac{a^2+b^2}{b^2+c^2}=\frac{a^2+ac}{ac+c^2}=\frac{a(a+c)}{c(a+c)}=\frac{a}{c}[/tex], co kończy dowód.
Zad. 2. Ekipy, pracując osobno, w jeden dzień wyremontują odpowiednio 1/12, 1/15 i 1/8 część mieszkania. Sumując te ułamki, dostajemy 33/120 = 11/40. Oznacza to, że gdyby ekipy pracowały razem, to w jeden dzień wyremontują 11/40 mieszkania. Natomiast całe mieszczanie wyremontują, pracując 40/11 raza dłużej, czyli pracując 3 i 7/11 dnia lub inaczej 3 dni, 15 godzin, 16 minut i 21,82 sekundy.
Zad. 3. Miara kąta CED wynosi 90o. Zauważmy, że trójkąty ADE i BCE są równoramienne i mamy |AE|=|AD|=|BE|=|BC|. Stąd równe są miary kątów AED i ADE oraz miary kątów BEC i BCE. Ponieważ suma kątów w trójkącie wynosi 180o, |∡DAE| =180°-2·|∡AED|. Podobnie |∡CBE| = 180°-2·|∡BEC|. Ponieważ suma sąsiednich kątów równoległoboku wynosi 180°, |∡DAE|+|∡CBE| = 180°, czyli |∡AED|+|∡BEC| = 90°. Stąd już łatwo zauważyć, że kąt CED ma 90°, bo razem z kątami AED i BEC tworzą kąt półpełny.

 Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć? Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
 Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera.
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 

