Zad. 1. W klasie znajdują się ławki w kształcie trapezu równoramiennego będącego połową sześciokąta foremnego. Przy każdym z krótszych boków może usiąść jedna osoba, a przy dłuższym - dwie. Dwie ławki można zestawić, tworząc miejsca dla 6 lub 8 osób, jak na rysunku.
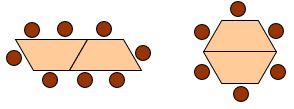
Ile ławek trzeba zestawić i jak, aby mogło usiąść przy nich dokładnie 10 osób? Naszkicuj tę sytuację.
Zad. 2. Odcinek o długości 12 cm podzielono czterema punktami wewnętrznymi na odcinki o równej długości. Jaką długość ma każdy z tych odcinków?
Zad. 3. W koszykówce punkty otrzymuje się za umieszczenie piłki w koszu:
- 1 pkt za celny rzut wykonany z linii rzutów wolnych,
- 2 pkt. za celny rzut wykonany z wnętrza obszaru ograniczonego linią rzutów za trzy punkty,
- 3 pkt. za celny rzut wykonany spoza obszaru ograniczonego linią rzutów za trzy punkty.
Koszykarz zdobył w meczu 34 punkty w 14 rzutach, w tym jeden z linii rzutów wolnych. Ile wykonał rzutów za 2 punkty?
W marcu punkty zdobyli:
- 3 pkt. – Klara Bartkowska SP 107 Wrocław, Bartosz Bębenek SSP Szprotawa, Jakub Błaszkiewicz SP 6 Jelenia Góra, Ewa Bogacz SP Smolec, Artur Bumażnik SP 1 Piechowice, Zuzanna Buraczewska SP 107 Wrocław, Jakub Cecuła SP 4 Grodzisk Wielkopolski, Natalia Czurejno SP Wykroty, Jan Czyrnek SP Załuczne, Piotr Dyl SP Łochowo, Michał Fudala SP Załuczne, Mateusz Galik SP Arka Wrocław, Michał Gatlik SP Skawinki, Amelia Gorzkowska SP Binarowa, Michał Gomulski SP 8 Oleśnica, Maciej Hryniewicz SP 9 Gliwice, Marcel Janicki SSP Stabkowice, Marika Kaczmarczyk SP 5 Kielce, Alicja Kaliszewska SP 1 Brzeg Dolny, Jakub Kaszewski SP 2 Jelenia Góra, Klara Kogut SP 9 Gliwice, Wiktoria Kornaus SP 42 Wrocław, Bruno Kowal SP 5 Brzeg, Filip Kowalski SP Mirków, Wiktoria Kozak SP Raniżów, Maja Kus SP 42 Wrocław, Piotr Laszkiewicz SP 11 Jelenia Góra, Zofia Lech SSP Stabkowice, Paulina Lichoń SP Biedrzychowice, Aleksandra Malicka SP 37 Szczecin, Mateusz Małecki SP 5 Brzeg, Patryk Mańka SP Miękinia, Weronika Michałowska PSP 1 Białystok, Paweł Nowak SP Mazury, Joanna Nowakowska SP 3 Głogów, Dorota Owczarek SP 42 Wrocław, Olaf Pawka SP Józefów n. Wisłą, Bartosz Pawlaczyk SP 107 Wrocław, Maciej Pisowacki SP Mieroszów, Jan Płonka SP Trzebownisko, Agnieszka Płudowska SP 18 Lubin, Aleksander Porębny SP 113 Wrocław, Oliwia Raszewska SP 6 Boguszów-Gorce, Miłosz Schroeder SP 42 Wrocław, Alicja Siomka SP Lewin Brzeski, Igor Siry SP 2 Legionowo, Michał Snoch SP Zachorzów, Nadia Stefanowska SP 10 Legnica, Anna Stępień SP Binarowa, Dawid Stępień SP 15 Opole, Zofia Strzelec SP 4 Wrocław, Domminik Szczygieł SP 42 Wrocław, Alicja Szwarczyńska SP Kowalowa, Maksymilian Tyburczy SP Mazury, Oliwia Urbanek SP 6 Brzeg, Oliwia Warenica SP 5 Łódź, Filip Tolarz SP 16 Wodzisław Śląski, Zuzanna Wąs SP 107 Wrocław, Kacper Wereszczyński SP Mieroszów, Julia Wilk SP Mazury, Karolina Winczura SP 9 Gliwice, Maciej Wiśniewski SSP Stabkowice, Szymon Wróblewski SP 5 Opole, Piotr Wodonos SP 42 Wrocław, Anastasiia Yakovleva SP 3 Mogilno, Franciszek Zakrawacz SP 2 Wałbrzych, Miłosz Zakrzewski SP Gostycyn, Dawid Zarębski SP Zachorzów, Oksana Zatwardnicka SP 28 Wałbrzych, Tomasz Zawadzki SP Wodzisław, Martyna Zymek SP 5 Brzeg;
- 2,5 pkt. –Kornelia Partyka SP Mazury, Malwina Milewska SP 9 Gliwice;
- 2 pkt. – Ryszard Augustyn SP 5 Brzeg, Martyna Chomaniec SP 5 Brzeg, Jakub Dopierała SP 5 Brzeg, Aurelia Karpińska SP 187 Warszawa, Matylda Karpińska SP 187 Warszawa, Hubert Klinik SP 9 Gliwice, Szymon Kopanicki SP 53 Częstochowa, Kaja Krajewska SP Jugów, Ziemowit Krzykowski SP 5 Brzeg, Amelia Rzeszutek SP Mazury, Jan Seweryn SP Złoty Stok, Szymon Sternal SP 9 Gliwice, Bartłomiej Suleja SP 42 Wrocław, Kinga Zakowicz SP 5 Brzeg, Maja Zielińska SP 5 Brzeg;
- 1,5 pkt. – Olgierd Żmijewski SP 2 Suchy Las.
Pozostali uczestnicy otrzymali poniżej 1 punktu
Zad. 1. Blat ławki jest połową sześciokąta, czyli trapezem równoramiennym, którego jedna z podstaw przystaje do ramienia, a druga stanowi jej dwukrotność. Kąty tego trapezu mają 60° lub 120°. Przy jednej ławce może usiąść 5 osób. Dołączając kolejną ławkę, zyskujemy 1 lub 3 miejsca (gdy złączenie ławek zablokuje odpowiednio 2 lub 1 miejsce). Zestawiając dwie ławki, otrzymamy 6 lub 8 miejsc siedzących.
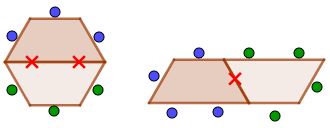
5+(3–2) = 5+1 = 6 5+(4–1) = 5+3 = 8
Gdy połączymy 4 ławki, uzyskamy 10 miejsc, bo 8+1+1 = 10 oraz 6+3+1 = 10. Zauważmy, że 6+1+1+1+1=10, ale taka sytuacja nie jest możliwa. Niżej przedstawiamy niektóre możliwe sytuacje połączenia 4 ławek.
Zad. 2. Koniec jednego odcinka jest początkiem następnego odcinka, zatem odcinek długości 12 cm podzielono na 5 części, skąd 12:5 = 2,4 cm.
Zad. 3. Koszykarz zdobył 1 punkt za rzut z linii rzutów wolnych, zatem pozostałe 33 punkty zdobył w 13 rzutach za 2 lub 3 punkty. Oznaczmy przez x liczbę rzutów za 2 punkty. Wówczas liczba rzutów za 3 punkty wynosi 13–x. Łącznie liczba punktów za 2 lub 3 punkty wynosi 2x+3(13–x) = 33, skąd x=6.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
