Zad. 1. Gdzie na płaszczyźnie leżą punkty, których współrzędne spełniają nierówność x2+2y+3y2 ≥ 2xy-1 ?
Zad. 2. 28% kobiet i 23% mężczyzn pracujących w pewnej firmie mówi po hiszpańsku, a 15% wszystkich pracowników zna francuski. Ilu co najmniej pracowników liczy ta firma?
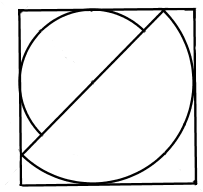
Zad. 3. Na rysunku przedstawiono kwadrat jednostkowy i dwa półokręgi styczne do jego boków. Średnica większego z nich jest prostopadła do przekątnej kwadratu. Jaki jest promień mniejszego półokręgu?
Część Ligowiczów nie udzieliła odpowiedzi na pytanie z zad. 1. (Pisali tylko, że nierówność jest spełniona dla dowolnych x i y).
Maksymalną ocenę 3 pkt za rozwiązania zadań październikowych zdobyło jednak aż 21 Ligowiczów: Adam Balawender, Agnieszka Ćmiel, Piotr Derda, Aleksandra Grzelak, Justyna Kręcichwost, Karolina Łagoda, Karol Łukasik, Przemysław Michałek, Marek Mika, Martyna Mikoda, Dorota Mularczyk, Ngoc Khanh Nguyen, Michał Opiełka, Bartosz Pawliczak, Michał Stroka, Dominik Strzyż, Patrick Szmucer, Wojciech Tobiś, Aleksander Ulatowski, Karol Wachtarczyk i Arkadiusz Wróbel.
Po 2,5 pkt uzyskali: Alexander Dulak, Agata Filipowicz, Grzegorz Kowalczyk, Magda Madera, Ewa Pojasek, Tomasz Skalski i Jakub Sobyra.
Gratulujemy wszystkim!
Zad. 1. Dana nierówność to równoważnie: (x–y)2+y2+(y+1)2 ≥ 0, więc spełniają ją współrzędne wszystkich punktów płaszczyzny.
Zad. 2. 28% liczby kobiet, 23% liczby mężczyzn i 15% wszystkich to oczywiście liczby całkowite, więc liczba zatrudnionych kobiet musi dzielić się przez 25 (bo 28% to nieskracalne 7/25), liczba mężczyzn - przez 100 (analogicznie) i wreszcie liczba wszystkich - przez 20. Jeśli przyjąć raczej naturalne założenie, że z danych wynika, że w firmie pracują zarówno kobiety jak i mężczyzni, to należy znaleźć najmniejszą liczbę postaci 25a+100b, gdzie a i b są całkowite dodatnie, która dzieli się przez 20. Zatem a musi dzielić się przez 4 i najmniejsze możliwe a i b (4 i 1) dają odpowiedź: 200 pracowników.
Zad. 3. Jeśli przez wspólny środek półokręgów poprowadzić proste równoległe do boków kwadratu, to przetną je one w punktach styczności półokręgów z bokami i łatwo można wówczas zauważyć, że długość boku kwadratu to suma długości promieni półokręgów, czyli 1 = r + R. Jednocześnie górny odcinek pionowej z poprowadzonych prostych jest promieniem mniejszego półokręgu i tworzy z promieniem większego oraz odcinkiem górnego boku kwadratu trójkąt prostokątny równoramienny, zatem R = r√2.
Odp.: r = 1/√2+1 = √2–1.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
