Zad. 1. Ile współczynników wymiernych zawiera rozwinięcie dwumianu [tex](\sqrt{3}x+\sqrt[4]{7}y)^{80}[/tex]?
Zad. 2. Na egzaminie student losuje dwa pytania i jeśli na oba odpowie dobrze, to zdaje egzamin. Jeśli tylko na jedno z pytań odpowie dobrze, to losuje trzecie pytanie i tylko poprawna odpowiedź na nie pozwoli mu zdać egzamin. W pozostałych przypadkach student nie zdaje egzaminu. Jakie jest prawdopodobieństwo, że student zda egzamin, jeśli zna odpowiedzi na 18 spośród 30 pytań egzaminacyjnych?
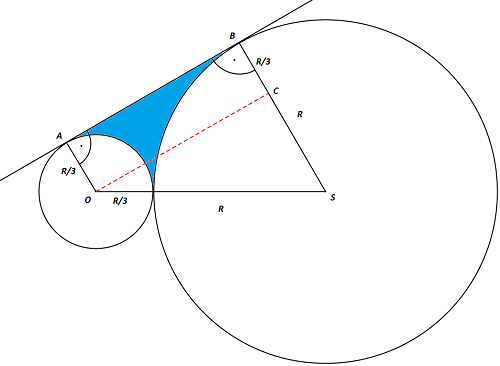
Zad. 3. Dwa okręgi o promieniach R i R/3 styczne zewnętrznie, posiadają wspólną styczną nieprzechodzącą przez punkt styczności tych okręgów. Oblicz pole figury ograniczonej tymi okręgami i wspomnianą styczną.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Krzysztof Bednarek III LO Wrocław, Kamila Bojar ZSP Szprotawa, Konrad Budzyński IX LO Wrocław, Bartosz Czyżewski I LO Jelenia Góra, Kamil Demczyszyn VI T Wrocław, Rafał Łyżwa I LO Dzierżoniów, Szymon Meyer II LO Opole, Piotr Paduszyński SLO Żary, Konrad Piechota IX LO Wrocław, Kacper Puchacewicz I LO Zielona Góra, Tomasz Stempniak I LO Ostrów Wielkopolski i Wojciech Wiśniewski I LO Giżycko,
- 2,5 pkt. - Maciej Golec IX LO Wrocław,
- 2 pkt. - Robert Czwartosz LO Trzebnica, Piotr Jażdżewski I LO Oleśnica, Antoni Kamiński III LO Wrocław, Kacper Klecuń XIV LO Wrocław, Łukasz Ptak III LO Wrocław i Magdalena Stroka II LO Opole,
- 1 pkt. - Martyna Cisakowska XIV LO Wrocław, Krzysztof Danielak I LO Jelenia Góra, Zuzanna Raszczyk VIII LO Wrocław i Marta Smykała ZSO Głubczyce.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Zad. 1. Wymiernych współczynników jest 21. Korzystając z rozwinięcia dwumianowego Newtona, dostajemy [tex](\sqrt{3}x+\sqrt[4]{7}y)^{80}=\sum_{k=0}^{80}(\sqrt{3}x)^{80-k}(\sqrt[4]{7}y)^k[/tex]. Pierwszy czynnik jest wymierny dla wykładników parzystych, a drugi - tylko dla wykładników podzielnych przez 4. Liczb podzielnych praz 4 w zbiorze {0, 1, 2, ..., 80} jest 21 i tyle jest wymiernych współczynników.
Zad. 2. Prawdopodobieństwo to wynosi 663/1015, czyli około 0,6532. Student zda egzamin, gdy odpowie poprawnie na oba pytania w pierwszym losowaniu (prawdopodobieństwo równe 18·17/30·29), lub gdy odpowie tylko na jedno z dwóch pytań poprawnie i na trzecie pytanie (prawdopodobieństwo równe 2·12·17·18/30·29·28). Dodając te liczby, dostajemy prawdopodobieństwo zdania egzaminu równe 663/1015.
Zad. 3. Pole tej figury to R2· (24√3-11π)/54. Zauważmy, że pole szukanego obszaru obliczymy jako różnicę pól trapezu ABSO i dwóch wycinków kół. Aby obliczyć pole trapezu, musimy wyznaczyć długość odcinka AB, a on przystaje do odcinka OC. Korzystając z twierdzenia Pitagorasa dla trójkąta OSC, dostajemy |AB|=|OC|=2R√3/3. Stąd pole trapezu wynosi PABSO=(R+R/3)/2·2R√3/3=4√3/9·R2. Ponieważ długość przyprostokątnej CS w trójkącie OSC jest równa 2R/3, a długość przeciwprostokątnej OS wynosi 4R/3, czyli jest dwa razy dłuższa, mamy do czynienia z połową trójkąta równobocznego i kąt OSC ma miarę 60o. Stąd miara kąta AOS wynosi 120o. Pole wycinka mniejszego koła wynosi R2·π/27, a pole wycinka większego koła R2·π/6. Pole figury oznaczonej kolorem niebieskim wynosi zatem 4√3/9·R2-R2·π/27-R2·π/6 = R2· (24√3-11π)/54.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
