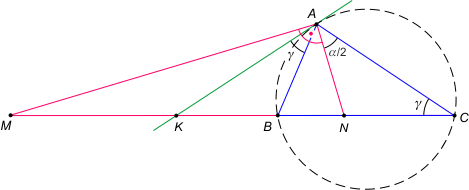
Zad. 1. Przez wierzchołek A trójkąta ostrokątnego ABC poprowadzono styczną AK do okręgu opisanego na tym trójkącie. Niech AN i AM będą dwusiecznymi odpowiednio kąta A i kąta doń przyległego, przy czym K, N, M leżą na prostej BC. Wykaż, że |MK| = |KN|.
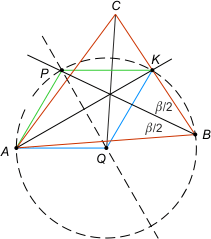
Zad. 2. Niech AK będzie dwusieczną kąta A (o mierze α) w trójkącie ABC, przy czym K leży na BC, a punkty P i Q leżą na pozostałych dwusiecznych, tak że |PA| = |PK| oraz |QA| = |QK|. Wykaż, że |∡PAQ| = 90°–α/2.
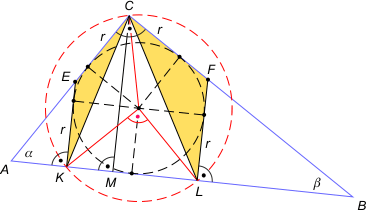
Zad. 3. Dany jest trójkąt prostokątny i okrąg weń wpisany. Pod jakim kątem widać rzut prostokątny tego okręgu na przeciwprostokątną z wierzchołka kąta prostego ?
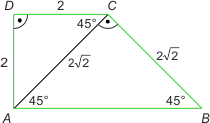
Zad. 4. (wolna amerykanka) W trapezie ABCD kąty A i D są proste. Wiedząc, że długość przekątnej AC wynosi 2√2, |∡ACB|= 90° oraz |∡ACD| = 45°, oblicz długość wektora CB – CA + CD.
Dziękujemy stałym uczestnikom Ligi za rozwiązania zadań i witamy w tym gronie nowych miłośników geometrii. Oto wyniki październikowe.
Za zadania 1 - 3 maksymalną liczbę 30 punktów uzyskali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Jakub Gajdecki (uczeń,VIII LO Katowice), Iwona Gruszecka (nauczyciel, G 42 Warszawa), Mateusz Klein (uczeń, III LO Gdynia), Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas (student, PW), Wioleta Pilzak (studentka, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Sabina Khady Sy (studentka, UJ).
Zadanie 4 poprawnie rozwiązali i otrzymali 10 punktów: Jacek Bagiński, Włodzimierz Bąk, Jakub Gajdecki, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Sabina Khady Sy, Michał Szymański (student, PWr), Wojciech Tomiczek (inżynier, Lipowa).
Gratulacje.
Zad. 1. Zauważmy, że |∡MAN|=90°, bo dwusieczne kątów przyległych są prostopadłe. W trójkącie AKN zachodzi |∡ANK| = γ+α/2 jako kąt zewnętrzny w trójkącie ANC. Natomiast kąt NAK jest sumą kątów BAK i NAB o mierze α/2. Zauważmy, że kąt BAK jest dopisany do okręgu i oparty na łuku AB, więc ma miarę γ (jak kąt ACB - wpisany, oparty na tym samym łuku) Zatem kąty ANK i NAK mają równe miary, a trójkąt AKN jest równoramienny i |AK|=|KN|. Rozważmy teraz trójkąt AKM. Zachodzi |∡KAM| = 90°–|∡KAN| oraz |∡AMK| = 90°–|∡ANK|, co wobec równości odejmowanych kątów daje |∡KAM|=|∡AMK|. Zatem trójkąt AKM też jest równoramienny i |AK|=|KM|. Z przechodniości równości mamy |KM|=|KN|.
Zad. 2. Zauważmy, że prosta PQ jest symetralną odcinka AK. Rozważmy okrąg opisany na trójkącie ABK. Prosta PQ dzieli łuk AK na połowy. Podobnie czyni dwusieczna kąta B. Wynika stąd, że punkt P leży na okręgu i |∡PAK| = β/2. Zauważmy, że punkt P jest wyznaczony jednoznacznie, bo dwusieczne kątów trójkąta nie są równoległe ani prostopadłe. Analogicznie otrzymujemy, że |∡QAK| = γ/2. Stąd |∡PAQ| = β/2+γ/2 = 90°–α/2.
Zad. 3. Przedstawimy dwa sposoby rozwiązania.
I sposób. Zauważmy, że |CO|=|OK|=|OL| = r√2, zatem punkty C, K i L leżą na okręgu o środku w O. Ponieważ kąt środkowy KOL jest prosty, kąt wpisany KCL ma 45°.
II sposób. Zauważmy, że trójkąty CEK i CFL są równoramienne. Niech CM będzie wysokością trójkąta ABC. Wówczas kąty KCM, EKC i ECK mają równe miary. Podobnie kąty MCL, CLF i LCF mają równe miary. Stąd |∡KCL| = |∡KCM|+|∡MCL| = 1/2|∡ACB| = 45°.
Zad. 4. Skorzystamy z własności iloczynu skalarnego wektorów mówiącej, że kwadrat skalarny wektora jest równy kwadratowi jego długości, tzn. |u|2= u2.
|CB–CA+CD|2 = (CB–CA+CD)º(CB–CA+CD) = CB2+CA2+CD2–2CBºCA+2CBºCD–2CAºCD = 8+8+4–2·0+2·2√2·2·(-√2/2)–2·2√2·2·√2/2 = 4. Stąd |CB–CA+CD| = 2.
Uwaga
A co jeśli trójkąt ABC jest równoramienny, a kąt A jest przeciwległy do podstawy? Wtedy zadanie nie ma rozwiązania.