Zad. 1. Nazwijmy liczbę naturalną szczęśliwą, jeśli suma jej cyfr dzieli się przez 17 oraz suma cyfr liczby o 10 większej też dzieli się przez 17. Jaka jest najmniejsza liczba szczęśliwa?
Zad. 2. Czy trójkąt leżący całkowicie we wnętrzu innego trójkąta musi mieć mniejszy obwód od tego zewnętrznego trójkąta?
Zad. 3. Co jest większe: √2√3 czy √3√2 ?
W tym miesiącu punkty zdobyli:
- 3 - Wiktor Baranowski II LO Bolesławiec, Bartosz Czyżewski I LO Jelenia Góra, Kacper Grela I LO Bolesławiec, Dawid Hanrahan I LO Brzeg, Dariusz Jajeśniak II LO Kraków, Beata Janiak III LO Opole, Michał Kępiński Społeczne LO Żary, Alina Langa I LO Oleśnica, Szymon Meyer II LO Opole, Mateusz Rzepecki III LO Wrocław, Николай Шамаев (Mykola Shamaiev) 131 szkoła Charków Ukraina, Tomasz Stempniak I LO Ostrów Wielkopolski, Kinga Wasilewska II LO Grudziądz i Wojciech Wiśniewski I LO Giżycko;
- 2 - Krzysztof Bednarek III LO Wrocław, Natalia Jach VIII LO Wrocław, Błażej Mrzygłód Publiczne V T Opole, Krzysztof Ratajczak ZSO Góra i Kinga Wróblewska VIII LO Wrocław;
- 1 - Konrad Bratek I LO Lwówek Śląski, Kamil Demczyszyn VI T Wrocław, Elżbieta Gontarz I LO Oleśnica i Agata Zielazna III LO Ostrów Wielkopolski.
Zad. 1. Najmniejszą liczbą szczęśliwą jest 7999. Niech s(n) oznacza sumę cyfr liczby n. Cyfrą dziesiątek szukanej liczby musi być 9, bo w przeciwnym razie s(n+10) = s(n)+1 i nie zajdzie podzielność. Wówczas cyfrą setek też musi być 9, bo w przeciwnym razie s(n+10) = s(n)–8 i też podzielność nie zajdzie. Jeśli cyfrą tysięcy nie jest wtedy 9, to s(n+10) = s(n)-17 i podzielność mogłaby zajść. Szukamy więc liczby postaci B99A, o sumie cyfr podzielnej przez 17, ale większej niż 18. Niech ta suma będzie najmniejsza możliwa, czyli 34, skąd B+A = 16 = 8+8 = 7+9. Z tych możliwości tworzymy najmniejszą możliwą liczbę.
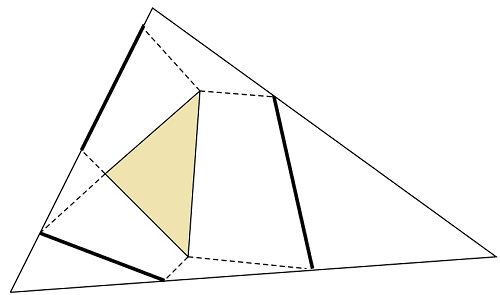
Zad. 2. Trójkąt wewnętrzny musi mieć mniejszy obwód niż zewnętrzny. Z wierzchołków wewnętrznego trójkąta prostopadle do jego boków prowadzimy odcinki do przecięcia z brzegiem zewnętrznego trójkąta. Odcinki pogrubione mają w sumie długość większą od obwodu lub równą obwodowi wewnętrznego trójkąta. Teraz jeszcze do każdego z pogrubionych odcinków, które nie leżą na obwodzie zewnętrznym, stosujemy nierówność trójkąta, porównując te odcinki z fragmentami obwodu zewnętrznego trójkąta i otrzymujemy tezę.
Zad. 3. Zachodzi √2√3 < √3√2. Podnosimy nierówność stronami do potęgi √6. Znak nierówności będzie zachowany, bo funkcja x√6 dla dodatnich argumentów jest rosnąca.
Otrzymujemy [tex]8^{\sqrt2{/}2}<
9^{\sqrt3{/}2}[/tex], a to kończy dowód, bo z prawej strony większe są jest jednocześnie podstawa i wykładnik.







