Zad. 1. Dla jakiej wartości x liczby log2, log(2x–1) i log(2x+3) tworzą ciąg arytmetyczny?
Zad. 2. Do jakiej potęgi n należy podnieść dwumian (a+x), aby współczynnik przy x2 był równy 66?
Zad. 3. Środki czterech kół o promieniu r znajdują się w wierzchołkach kwadratu o boku r. Ile wynosi pole części wspólnej tych czterech kół?
W tym miesiącu punkty zdobyli:
- 3 - Konrad Bratek I LO Lwówek Śląski, Bartosz Czyżewski I LO Jelenia Góra, Kamil Demczyszyn Lotnicze zakłady Naukowe Wrocław, Dawid Hanrahan I LO Brzeg, Dariusz Jajeśniak II LO Kraków, Piotr Jażdżewski I LO Oleśnica, Szymon Meyer II LO Opole, Николай Шамаев 131 Szkoła Ogólnokształcąca Charków (Ukraina), Tomasz Stempniak I LO Ostrów Wielkopolski i Wojciech Wiśniewski I LO Giżycko;
- 2 - Kamila Bojar ZSP Szprotawa, Kacper Grela I LO Bolesławiec, Michał Kępiński SLO Żary, Karol Kowalski I LO Kraków, Alina Langa I LO Oleśnica, Błażej Mrzygłód Technikum nr 5 Opole, Natalia Okopna VII LO Wrocław, Rafał Pych LO Leżajsk, Mateusz Rzepecki III LO Wrocław i Maksymilian Szcześniak LO Płock;
- 1 - Krzysztof Bednarek III LO Wrocław, Elżbieta Gontarz I LO Oleśnica i Beata Janiak III LO Opole.
Pozostałym uczestnikom nie przyznano punktów.
Po dwóch miesiącach Ligi Zadaniowej z wynikiem 6 pkt. (na 6 możliwych) prowadzą: Bartosz Czyżewski, Dawid Hanrahan, Dariusz Jajeśniak, Szymon Meyer, Николай Шамаев, Tomasz Stempniak i Wojciech Wiśniewski, drugie miejsce z wynikiem 5 pkt. zajmują: Kacper Grela, Michał Kępiński, Alina Langa i Mateusz Rzepecki, a trzecie miejsce z wynikiem 4 pkt. zajmują: Konrad Bratek, Kamil Demczyszyn, Beata Janiak i Błażej Mrzygłód. Gratulujemy!
Zad. 1. Dla x = log25.
Zad. 2. Ponieważ [tex](a+x)^n={{n}\choose{0}}a^n+{{n}\choose{1}}a^{n-1}x+{{n}\choose{2}}a^{n-2}x^2+\ldots+{{n}\choose{n}}x^n[/tex],
zachodzi n(n-1)/2 = 66, skąd n=12.
Zad. 3. Pole części wspólnej wynosi 1/3 r2(π+3–3√3) ≈ 0,3151r2.
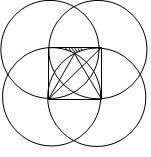
Zaczynamy od obliczenia pola soczewki będącej częścią wspólną dwóch kół. Połowa soczewki jest różnicą ćwiartki koła i trójkąta prostokątnego, więc pole soczewki wynosi 2(1/4πr2–1/2r2). Policzymy teraz pole części zakreskowanej, która pozostanie z kwadratu po odjęciu trójkąta równobocznego oraz dwóch wycinków kołowych o kącie 30°, czyli stanowiących 1/12 koła. Pole tej figury wynosi więc r2 – r2√3/4 – 1/12πr2. Teraz obliczymy pole jednej z dwóch części, które zostają z soczewki po odjęciu części wspólnej wszystkich kół. W tym celu od połowy kwadratu odejmiemy pół soczewki i dwie zakreskowane figury, otrzymując
1/2r2 – (1/4πr2–1/2r2) – 2(r2 – r2√3/4 – 1/12πr2).
Teraz wystarczy od pola soczewki odjąć podwojone obliczone właśnie pole. Po uproszczeniu otrzymamy wynik.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
