Zad. 1. Dla jakich wartości parametru a poniższy układ równań ma rozwiązanie?
[tex]
\begin{cases}
\sin x \cdot \sin y = 0,5 \\
\cos x\cdot \cos y=a \end{cases}
[/tex]
Zad. 2. Udowodnij, że ciąg [tex]a_n=\frac{2^n}{n!}[/tex], dla n>1 jest malejący.
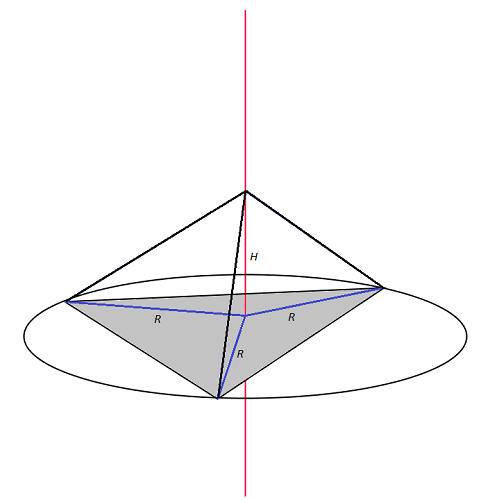
Zad. 3. Jaką figurę tworzą punkty przestrzeni, które są równo oddalone od wierzchołków pewnego trójkąta?
W tym miesiącu 3 pkt. zdobyli: W październiku punkty zdobyli:
- 3 - Dawid Migacz I LO Tarnów, Błażej Mrzygłód V Technikum Opole, Mikołaj Pater III LO Opole, Paweł Wesołowski II LO Końskie
- 2,5 - Bartosz Czyżewski I LO Jelenia Góra, Karol Kowalski I LO Kraków
- 2 - Beata Janiak III LO Opole, Mateusz Kwieciński I LO Bolesławiec, Joanna Lisiowska XXI LO Warszawa, Wojciech Wiśniewski I LO Giżycko
- 1,5 - Konrad Bratek I LO Bolesławiec, Sebastian Janus I LO Oleśnica, Michał Korman V LO Kraków, Monika Marusiak I LO Bolesławiec, Cyprian Skóra ZSO Głubczyce,
- 1 - Magdalena Gołębiowska III LO Kalisz, Kacper Mazurkiewicz I LO Zduńska Wola.
Pozostałym uczestnikom przyznano poniżej 1 pkt.
Zad. 1. Zauważmy, że -1≤a≤1, ponieważ funkcja kosinus nie przyjmuje wartości spoza tego zakresu. Dodając i odejmując stronami równania układu oraz korzystając z zależności
sinxsiny+cosxcosy = cos(x–y), sinxsiny–cosxcosy = -cos(x+y),
dostaniemy cos(x–y) = a+0,5 oraz cos(x+y) = a–0,5.
Stąd -1 ≤ a+0,5 ≤ 1 i -1 ≤ a–0,5 ≤ 1, czyli -1,5 ≤ a ≤ 0,5 i -0,5 ≤ a ≤ 1,5.
Uwzględniając oba warunki, otrzymujemy odpowiedź: układ równań ma rozwiązanie dla -0,5 ≤ a ≤ 0,5.
Zad. 2. Rozważmy [tex]\frac{a_{n+1}}{a_{n}}=\frac{2^{n+1}}{(n+1)!}\frac{n!}{2^n}=\frac{2}{n+1}[/tex]<1. Stąd i z warunku, że wyrazy ciągu są dodatnie wnioskujemy, że ciąg jest malejący.
Zad. 3. Jest to prosta prostopadła do płaszczyzny zawierającej trójkąt, przechodząca przez środek S okręgu opisanego na tym trójkącie (o promieniu R). To że środek okręgu opisanego na trójkącie jest równo oddalony od jego wierzchołków jest oczywiste. Każdy inny punkt leżący na opisanej prostej i odległy od S o H, jest odległy od wierzchołków trójkąta o tyle samo, tzn. o √(R2+H2).