Zad. 1. Rozwiąż równanie [tex]2^{\sin^2x}-2^{\cos^2x}=1[/tex].
Zad. 2. Udowodnij, że sześcian długości przeciwprostokątnej w trójkącie prostokątnym jest większy od sumy sześcianów długości jego przyprostokątnych.
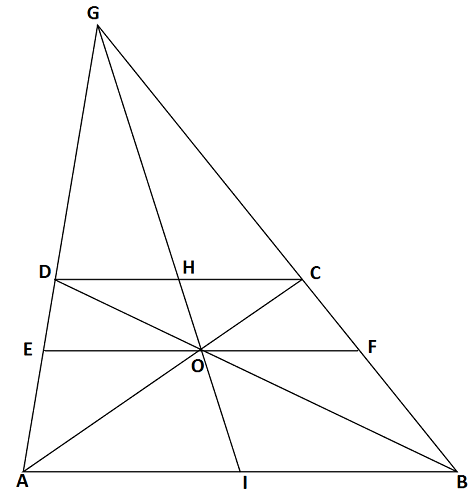
Zad. 3. Udowodnij, że prosta przechodząca przez punkt przecięcia przekątnych trapezu i punkt przecięcia przedłużeń boków nierównoległych, dzieli podstawy tego trapezu na połowy.
W październiku punkty zdobyli:
- 3 - Konrad Bratek I LO Bolesławiec, Bartosz Czyżewski I LO Jelenia Góra, Karol Kowalski I LO Kraków, Błażej Mrzygłód V Technikum Opole, Mikołaj Pater III LO Opole, Paweł Wesołowski II LO Końskie i Wojciech Wiśniewski I LO Giżycko;
- 2,5 - Monika Marusiak I LO Bolesławiec i Piotr Pojda ZSO Głubczyce;
- 2 - Joanna Lisiowska XXI LO Warszawa;
- 1,5 - Cyprian Skóra ZSO Głubczyce;
- 1 - Sebastian Janus I LO Oleśnica i Mateusz Kwieciński I LO Bolesławiec.
Pozostałym uczestnikom przyznano poniżej 1 pkt.
Po dwóch miesiącach Ligi Zadaniowej Szkół Ponadgimnazjalnych z wynikiem 6 pkt. (na 6 możliwych) prowadzą: Błażej Mrzygłód, Mikołaj Pater i Paweł Wesołowski.
Drugie miejsce z wynikiem 5,5 pkt. zajmują: Bartosz Czyżewski i Karol Kowalski.
Trzecie miejsce z wynikiem 5 pkt. zajmuje Wojciech Wiśniewski.
Gratulujemy!
Zad. 1. Równanie przekształcamy równoważnie:
[tex]2^{\sin^2x}-2^{1-\sin^2x}=1[/tex]
[tex](2^{\sin^2x})^2-2-2^{\sin^2x}=0[/tex]
Po dokonaniu podstawienia [tex]2^{\sin^2x}=t[/tex], dostajemy równanie t2–t–2 = 0, które jest równoważne (t+1)(t–2) = 0. Ponieważ t nie może być ujemne (dlaczego?), dostajemy [tex]2^{\sin^2x}=2[/tex], czyli sinx = 1 lub sinx = -1. Ostatecznie równanie spełniają liczby x = π/2+kπ, gdzie k jest liczbą całkowitą.
Zad. 2. Oznaczmy długości przyprostokątnych trójkąta przez a i b, a długość przeciwprostokątnej przez c. Z własności trójkąta prostokątnego mamy c>a i c>b. Stąd, mnożąc nierówności stronami odpowiednio przez a2 i b2, dostaniemy c·a2 > a3 i c·b2 > b3. Dodając je stronami oraz korzystając z twierdzenia Pitagorasa, otrzymujemy tezę: c3 > a3+b3.
Zad. 3. Z podobieństwa trójkątów DEO do ABD oraz CFO do ABC wynika, że |EO|=|OF|. Z Twierdzenia Talesa dostajemy |AI|/|EO| = |IB|/|OF|, a stąd |AI|=|IB|. Podobnie pokazujemy |DH|=|HC|.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
