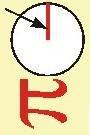
Zad. 1. Odległości punktu O leżącego wewnątrz trójkąta prostokątnego ABC od dwóch wierzchołków wynoszą p i q. Trójkąty AOB, BOC i AOC mają równe pola. Ile wynosi odległość punktu O od trzeciego wierzchołka?
Zad. 2. Niech H oznacza ortocentrum (tzn. punkt przecięcia wysokości) trójkąta ABC (ostrokątnego lub rozwartokątnego). Jaka jest miara kąta przy wierzchołku C, jeśli |HC| = |AB|?
Zad. 3. W trójkącie prostokątnym wysokość dzieli przeciwprostokątną na odcinki o długościach p i q. Ile wynosi suma długości promieni okręgów wpisanych we wszystkie trójkąty?
Zad. 4. (wolna amerykanka) Czworokąt ABCD jest wpisany w okrąg. Jakie ma pole, jeśli |AB| = |BC|, |BD| = a oraz |∡CDB| = γ?
Witam wszystkich 'starych' i nowych mistrzów geometrii. Życzę nieustającej satysfakcji z naszej wspólnej pasji.
Za rozwiązania zadań 1-3 punkty zdobyli:
- 30 - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Włodzimierz Bąk (nauczyciel akademicki UO), Zygmunt Krawczyk (nauczyciel, SLO Żary), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Michel Migas (student matematyki PW), Sławomir Matysik (nauczyciel matematyki, ZS nr 1 Trzebnica) , Tadeusz Porzucek (emerytowany nauczyciel, Gostyń) oraz Dominik Sulik (uczeń, I LO Kraków)
- 28 - Sabina Khady Sy (studentka nanotechnologii na UJ), Mikołaj Sikora( (student informatyki AGH)
- 22 - Tomasz Szczepanik (uczeń, I LO Kraków).
- 12 - Jakub Węgrecki (student filozofii, UJ)
Za zadanie 4 maksymalną liczbę 10 pkt. otrzymali: Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Mikołaj Sikora, Sabina Khady Sy, Jakub Węgrecki oraz Szymon Kaźmierowski. 8 pkt. otrzymał Dominik Sulik.
Zad. 1. Łatwo wykazać, że punkt O jest środkiem ciężkości trójkąta. Przedłużmy środkową CM3 tak, żeby |OM3| = |M3D|. Otrzymujemy równoległobok ADBO. Zauważmy, że |AB| = 2|CM3|, bo środkowa przeciwprostokątnej jest od niej dwa razy krótsza, oraz |OD| = |CO|, bo z własności środka ciężkości |OM3|=|CO|/2. Wystarczy teraz wykorzystać zależność między przekątnymi i bokami w równoległoboku: suma kwadratów długości przekątnych jest równa sumie kwadratów długości boków. Przyjmując |AO| = p oraz |OB| = q, otrzymujemy |CO|=|OD| = [tex]\frac{\sqrt{p^2+q^2}}{5}[/tex]. W pozostałych przypadkach otrzymujemy odległości [tex]\sqrt{5p^2-q^2}[/tex] oraz [tex]\sqrt{5q^2-p^2}[/tex].
Zad. 2. Niech ABC będzie trójkątem ostrokątnym. Przez jego wierzchołki prowadzimy proste równoległe do boków, otrzymując trójkąt A'B'C' podobny do wyjściowego w skali 2:1 (cecha kkk). Zauważmy, że punkt H jest środkiem okręgu opisanego na trójkącie A'B'C' (jako punkt przecięcia symetralnych boków tego trójkąta). Wobec założenia |AB| = |CA'| = |CB'| = |CH| mamy |∡B'HA'| =90°. Wówczas kąt wpisany B'C'A' ma miarę 45°, zatem |∡ACB| = 45°. Rozumując analogicznie w przypadku trójkąta rozwartokątnego (|∡ C|>90°), otrzymujemy |∡ACB| = |∡B'C'A'| = 135°. Gdy kąt B jest rozwarty, otrzymujemy |∡C| = 45°. Zauważmy, że wszystko zależy od tego, czy punkty H i C leżą po jednej czy po obu stronach prostej A'B'.
Zad. 3. Oznaczmy długości promieni okręgów wpisanych w trójkąty ADC, DBC i ABC odpowiednio przez r1, r2 i r. Otrzymujemy wówczas r1 + r2 + r = (|AD|+|CD|–|AC|)/2 + (|DB|+|CD|–|BC|)/2 + (|AC|+|CB|–|AB|)/2 = |CD|. CD jest wysokością opuszczoną na przeciwprostokątną, więc jej długość jest średnią geometryczną długości odcinków, na jakie dzieli ona przeciwprostokątną, zatem |CD| = √pq. Ostatecznie r1 + r2 + r = √pq.
Zad. 4. (wolna amerykanka) Na przedłużeniu boku CD poza punkt C odkładamy odcinek CE ≡ AD. Wówczas trójkąty ABD i BCE są przystające, bowiem AD ≡ CE, AB ≡ BC oraz ∡BCE ≡ ∡BAD, bo czworokąt ABCD jest wpisany w okrąg. Wynika stąd, że pole czworokąta ABCD jest równe polu trójkąta równoramiennego BED (mamy γ = |∡ADB| = |∡BEC|) i wynosi a2sin(180°– 2γ)/2 = (a2sin2γ)/2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
