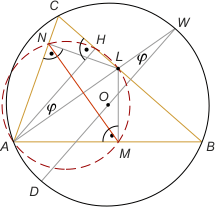
Zad. 1. Oblicz miary kątów w trójkącie, wiedząc że wysokość, dwusieczna i środkowa wychodzące z jednego wierzchołka, dzielą ten kąt na cztery równe części.
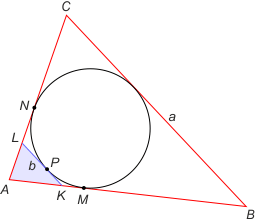
Zad. 2. W trójkącie ABC bok BC ma długość a. Odcinek stycznej do okręgu wpisanego w ten trójkąt równoległej do boku BC zawarty między bokami AC i AB ma długość b. Oblicz obwód trójkąta.
Zad. 3. Dany jest trójkąt ABC. Na półprostych AB i CB odłożono odcinki AK i CM o długości |AC|. Wykaż, że promień okręgu opisanego na trójkącie BKM jest równy odległości między środkami okręgów wpisanego w trójkąt i opisanego na trójkącie ABC.
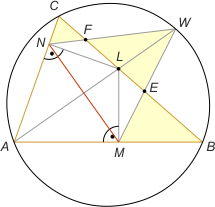
Zad. 4. (wolna amerykanka) Dwusieczna kąta A w trójkącie ABC przecina bok BC w punkcie L, a okrąg opisany na tym trójkącie w punkcie W. Niech M i N będą rzutami prostokątnymi punktu L odpowiednio na boki AB i AC. Niech MW przecina bok BC w punkcie E, a NW przecina bok BC w punkcie F. Wykaż, że suma pól trójkątów MEB i NFC jest równa polu trójkąta WEF.
Listopadowe zadania okazały się trudniejsze niż zazwyczaj. Za zadania 1-3 punkty zdobyli:
- 30 pkt - Włodzimierz Bąk (nauczyciel akademicki UO), Michel Migas (student matematyki PW) i Tadeusz Porzucek (emerytowany nauczyciel, Gostyń)
- 20 pkt - Jacek Bagiński (nauczyciel matematyki, I LO Kraków), Szymon Kaźmierowski (nauczyciel, IV LO Elbląg), Dominik Sulik (uczeń, I LO Kraków)
- 18 pkt - Tomasz Szczepanik (uczeń, I LO Kraków)
W kategorii wolnej amerykanki 10 punktów zdobyli: Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas, Tadeusz Porzucek, Mikołaj Sikora (student informatyki AGH) oraz Dominik Sulik.
Zad. 1. Niech H będzie spodkiem wysokości opuszczonej z wierzchołka C, L - spodkiem dwusiecznej kąta C, D - punktem przecięcia dwusiecznej CL z okręgiem opisanym na trójkącie, M - środkiem boku AB, a O - środkiem okręgu. Z założenia |∡HCL| = |∡LCM| = φ, więc wobec równoległości odcinków CH (wysokość) i OD (symetralna boku AB) mamy |∡CDM| = φ. Stąd trójkąt CDM jest równoramienny, a jego kąt ostry ma miarę φ. Z drugiej strony trójkąt COD również jest równoramienny i ma kąt ostry o mierze φ, co oznacza, że punkty M i O pokrywają się. AB jest zatem średnicą okręgu, a kąt C jest prosty. Ostatecznie miary kątów trójkąta ABC wynoszą 90º, 77,5° oraz 22,5°.
Zad. 2. Zauważmy, że |AM| = |AN| = p–a, gdzie p jest połową obwodu trójkąta ABC. Z założenia trójkąty ABC i AKL są podobne w skali k = a/b. Zauważmy, że wobec oczywistych równości |PK| = |KM| oraz |LP| = |LN|, obwód trójkąta AKL wynosi |AM|+|AN| = 2(p–a). Uwzględniając wartość skali podobieństwa, otrzymujemy obwód trójkąta ABC równy 2a2/(a–b).
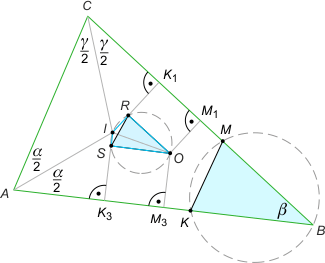
Zad. 3. Niech K1 i K 3 oznaczają punkty styczności okręgu wpisanego w trójkąt z bokami BC i AB, a M1 i M3 - środki tych boków. Zauważmy, że |CK1| = p–c oraz |CM1| = a/2, gdzie p jest połową obwodu trójkąta ABC. Stąd |K1M1| = (c–b)/2. Analogicznie |K3M3| = |AM3|–|AK3| =
c/2 – (p–a) = (a–b)/2. Przez środek okręgu opisanego na trójkącie prowadzimy równoległe do boków BC i AB przecinające promienie okręgu wpisanego IK1 oraz IK3 w punktach R i S odpowiednio. Zauważmy, że trójkąty ORS i KMB są podobne w skali k = 1/2, bo |KB| = c–b, |MB| = a–b i oba mają kąt β). Z drugiej strony na czworokącie OIRS można opisać okrąg, którego średnicą jest OI. Po uwzględnieniu skali podobieństwa trójkątów otrzymujemy tezę.
Zad. 4. Najpierw wykażemy, że pole trójkąta ABC wyraża się wzorem 1/2·|AW|·|MN| (rys. 1). Zauważmy, że trójkąty ALH i ADW są podobne, bo oba są prostokątne i AH jest równoległy do WD. Niech φ oznacza miarę kątów HAL i AWD. Zachodzi |AW| = 2R·cosφ. Na czworokącie AMLN można opisać okrąg, którego średnicą jest AL. Z twierdzenia sinusów w trójkącie AMN mamy |MN| = |AL|·sinα. Otrzymujemy 1/2·|MN|·|AW| = |AL|·sinα·R·cosφ = |AL|·cosφ·(|BC|/2R)·R (z twierdzenia sinusów w trójkącie ABC), a to jest równe 1/2·|AH|·|BC| (z proporcji trygonometrycznych w trójkącie AHL). A to jest pole trójkąta ABC. Teraz, korzystając z otrzymanego wyniku, udowodnimy tezę zadania. Łatwo zauważyć, że czworokąt AMLN jest deltoidem i jego przekątne są prostopadłe. Oznacza to, że pole czworokąta AMWN równe polu trójkąta ABC jest równe połowie iloczynu długości MN i AW. Wystarczy teraz zauważyć, że trójkąt ABC i czworokąt AMWN mają wspólną część, którą jest pięciokąt AMEFN. Stąd wynika teza.