Zad. 1. Znajdź liczby czterocyfrowe będące kwadratami o tej własności, że wszystkie ich cyfry można zmniejszyć o tę samą liczbę tak, że powstanie nowa liczba czterocyfrowa także będąca kwadratem.
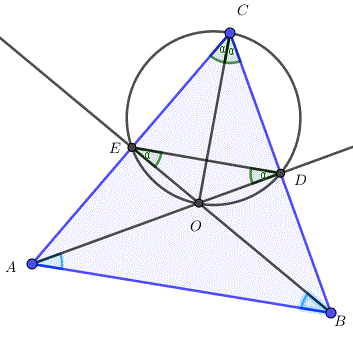
Zad. 2. W trójkącie ABC poprowadzono dwusieczne AD i BE (D∈BC, E∈AC) przecinające się w punkcie O. Wiadomo, że wierzchołek C leży na okręgu przechodzącym przez punkty E, D, O. Znajdź miary kątów trójkąta EDO.
Zad. 3. Rozpatrujemy wszystkie iloczyny liczb dwucyfrowych. Których iloczynów jest więcej: tych, które dają wyniki trzycyfrowe, czy tych, które dają wyniki czterocyfrowe? Odpowiedź uzasadnij.
W październiku punkty zdobyli:
- 3 pkt. – Dominik Bysiewicz I LO Krosno, Marek Chotnicki II LO Oleśnica, Jakub Jagiełła LO Politechnika Wr, Bartosz Kaczor I LO Głogów, Wiktoria Malinoska XXVII LO Warszawa, Aleksandra Miziołek ZS Libiąż, Laura Stefanowska KLO Legnica, Igor Wojtun I LO Głogów, Gabriela Wołynko I LO Węgrów;
- 2,5 pkt. – Kacper Woszczek II LO Wałbrzych, Adrian Chudzik I LO Leszno, Jakub Dobrzański I LO Lubin, Klaudia Hajduk ZSE Brzeg, Szymon Kowalcze ZSE Brzeg, Kasper Radom II LO Lubin, Natalia Siwek II LO Poznań, Aleksandra Strzelecka VIII LO Poznań, Wojciech Szwarczyński II LO Wałbrzych, Jerzy Wąsiewicz KLO Magdalenka;
- 2 pkt. – Konrad Leszczyński XIV LO Wrocław, Nina Sadziak VII LO Wrocław, Patrycja Zielińska I LO Żary;
- 1 pkt – Julia Kreis VII LO Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech m2 oznacza początkową liczbę czterocyfrową, 1000x+100x+10x+x=101.11x - liczbę odejmowaną, n2 - liczbę otrzymaną po operacji opisanej w treści zadania. Otrzymujemy równanie m2 – 101.11x = n2, skąd po przekształceniach (m–n)(m+n) = 101.11x. Zauważmy, że m<100 i n<100 (bo m2<1002=10000), więc m–n < 100 i m+n < 200. Stąd m+n = 101 i m–n = 11x. Z pierwszego równania otrzymujemy, że m i n są różnej parzystości, więc x jest nieparzyste. Mamy zatem
[tex] \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&11\end{array}\right.[/tex] lub [tex] \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&33\end{array}\right.[/tex] lub [tex] \left\{\begin{array}{rcl}m+n&=&101\\m-n&=&55\end{array}\right.[/tex] a stąd
[tex] \left\{\begin{array}{rcl}m&=&56\\n&=&45\end{array}\right.[/tex] lub [tex] \left\{\begin{array}{rcl}m&=&67\\n&=&34\end{array}\right.[/tex] lub [tex] \left\{\begin{array}{rcl}m&=&78\\n&=&23\end{array}\right.[/tex]
Trzeci układ jest sprzeczny z warunkiem n2>1000, czyli m2=562 lub m2=672. Szukane liczby to 3136 i 4489.
Zad. 2. Odcinek CO jest dwusieczną, więc |∡ECO| = |∡DCO| = α, stąd łuki EO i OD są przystające. Dalej |∡OED| = |∡ODE| = α (kąty wpisane oparte na tym samym łuku) oraz |∡EOD| = 180°—2α = |∡AOB| =180°–1/2(∡A+∡B) =180°–1/2(180°–2α) = 90°+α. Stąd 180°–2α = 90°+α, czyli α=30°. Zatem w trójkącie EDO mamy kąty E i D mają po 30°, a kąt O ma 120o.
Zad. 3. Liczb dwucyfrowych jest 90 (99–9 jednocyfrowych). Wszystkich iloczynów takich liczb jest więc 90 . 90 = 8100. Zauważmy, że jeżeli oba czynniki są większe od 31 (a takich czynników jest 68), to ioczyn jest większy lub równy 32 . 32 = 1024 i jest czterocyfrowy. Zatem takich iloczynów jest 68 . 68 = 4624, czyli więcej niż połowa z 8100, czyli więcej jest iloczynów czterocyfrowych.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
