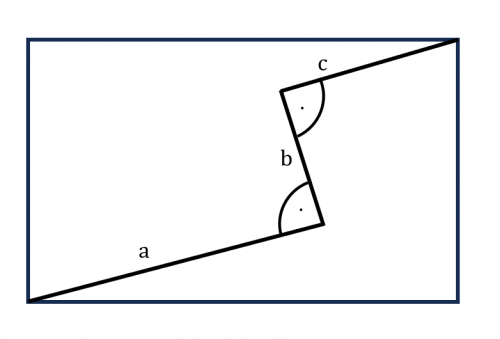
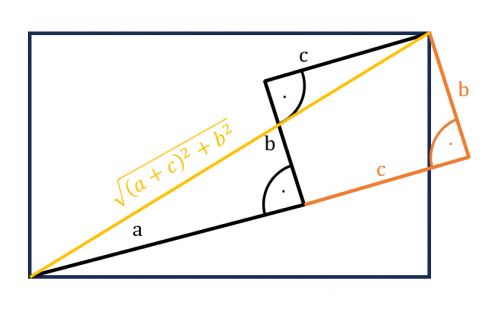
Zad. 1. Znajdź długość przekątnej prostokąta.
Zad. 2. Pokaż, że istnieje nieskończenie wiele liczb naturalnych n, których dwukrotność jest kwadratem, trzykrotność jest sześcianem, a pięciokrotność jest piątą potęgą jakiejś liczby naturalnej.
Zad. 3. Znajdź wszystkie trójki liczb naturalnych spełniające równanie 1/x + 1/y = z.
W październiku 18 pkt. zdobyli: Urszula Kwiatkowska (SP 221 Warszawa) i Szymon Michalik (SP 3 Przymierza Rodzin Warszawa).
Zad. 1. Rozwiązanie znajduje się na rysunku.
Zad. 2. Zacznijmy od rozważenia liczby n = 2a3b5c. By n spełniała warunki zadania, liczby a+1, b, c muszą być podzielne przez 2; liczby a, b+1, c muszą być podzielne przez 3; a liczby a, b, c+1 muszą być podzielne przez 5. Zauważamy, że jednym z rozwiązań jest a=15, b=20, c=24, więc m:= 215320524 spełnia warunki zadania. Ale dla p pierwszych i większych od 5 liczby postaci p30n także spełniają warunki zadania. Takich liczb pierwszych jest oczywiście nieskończenie wiele, zatem także liczb spełniających warunki zadania jest nieskończenie wiele.
Zad. 3. Lewa strona jest większa od 0 i nie większa od 2, wobec czego a to 1 lub 2 (przy czym a=2 tylko dla x=y=1). Gdyby x, y > 2, to 1/x + 1/y < 1. Załóżmy więc bez straty ogólności, że x=2. Wtedy y również musi być równe 2. Wobec powyższego istnieją dwa rozwiązania: x=y=2 oraz x=y=1.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
