Zad. 1. Znajdź wszystkie trójki liczb pierwszych p, q, r, których iloraz iloczynu i sumy wynosi 11.
Zad. 2. Ile jest dziewiątek w zapisie dziesiętnym liczby 999 999 9992?
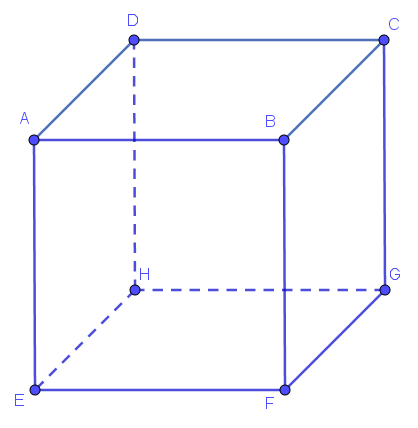
Zad. 3. Przez ile wierzchołków sześcianu może przechodzić sfera?
W październiku punkty zdobyli:
- 3 pkt. – Wojciech Domin III LO Wrocław, Wojciech Raszczuk ???;
- 2,5 pkt. – Emilia Cichowska II LO Lubin, Igor Wojtasik I LO Jelenia Góra;
- 2 pkt. – Adam Chowanek III LO Wałbrzych, Piotr Chybalski ZSP Kleszczów, Rafał Górzyński I LO Lubin, Bartosz Kaczor I LO Głogów, Kacper Krauze I LO Szczecinek, Kamil Pulik LO Międzyrzec Podlaski, Wiktoria Prokop II LO Głogów, Tomasz Smołka I LO Kraków, Michał Węgrzyn ALO PWr Wrocław, Igor Wojtun I LO Głogów;
- 1,5 pkt. – Karol Czajka II LO Oleśnica
- 1 pkt. – Martyna Gruszczyńska ???, Julia Leśniak LO Brzeg Dolny, Kinga Mielcarek II LO Oleśnica.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Podana równość po przekształceniu ma postać pqr = 11(p+q+r). Prawa strona dzieli się przez 11, więc lewa strona również musi dzielić się przez 11. Bez straty ogólności można przyjąć, że r = 11. Mamy wówczas 11pq = 11(p+q+11), czyli pq=p+q+11. Po przekształceniu otrzymamy q = 1+12/(p–1). Liczba p–1 musi być dzielnikiem 12, a wynik dzielenia musi być liczbą dodatnią. Mamy więc p–1 ∈ {1, 2, 3, 4, 6, 12}, czyli p ∈ {2, 3, 4, 5, 7, 13}. Warunki zadania spełniają liczby p=2 i q=13 lub p=3 i q=7. Szukane trójki to zatem (2, 11, 13) i (3, 7, 11).
Zad. 2. 9999999992 = (109–1)2 = ((10)9)2 – 2·109·1 + 12 = 1018 – 2·109 + 1. Liczba 1018 to jedynka i 18 zer, a 1018–2·109 to kolejno 8 dziewiątek, ósemka i 9 zer. Dodanie jedynki nie zmienia liczby dziewiątek. W zapisie 999 999 9992 jest więc osiem dziewiątek.
Zad. 3. Sfera może przechodzić przez jeden wierzchołek sześcianu, przez dwa (będące końcami krawędzi), przez trzy (leżące na jednej ścianie) lub przez cztery (tworzace ścianę). Jeśli przechodzi przez więcej niż cztery wierzchołki, to są wśród nich dwa będące końcami pewnej przekątnej sześcianu. Sfera przechodząca przez te dwa punkty i jeszcze przez co najmniej trzy inne wierzchołki jest opisana na trójkącie prostokątnym którego przeciwprostokątną jest przekątna sześcianu i jest ona jednocześnie średnicą tej sfery. Środek sfery leży więc w środku sześcianu sześcianu, czyli przechodzi ona przez wszystkie jego wierzchołki. Sfera może przechodzić przez 1, 2, 3, 4, lub 8 wierzchołków.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
