Zad. 1. Na ile sposobów można ustawić na szachownicy 4 wieże, tak aby żadna nie znalazła się w polu bicia innej?
Zad. 2. Ile w roku 2008 będzie takich dat, że zarówno numery dnia i miesiąca, jak i ich suma będą liczbami pierwszymi?
Zad. 3. Mrówka Kleofas podróżuje po linii układającej się w taki ślimak: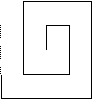 
(każde najbliższe równoległe odcinki leżą w odległości 1 cm). W jakiej odległości od położenia początkowego będzie Kleofas po przebyciu 2008 cm?
Najlepszym wynikiem miesiąca było rozwiązanie 3 zadań z jedną usterką, za co 2,5 pkt. zdobywa Michalina Sieradzka z Gimnazjum nr 49 we Wrocławiu. Gratulujemy!
Michalina prowadzi również w sumarycznej klasyfikacji Ligi (8,5 pkt. na 12 możliwych).
Zad. 1. Pierwszą wieżę możemy ustawić na dowolnym polu szachownicy, czyli możemy to zrobić na 64 sposoby. Dla drugiej pozostaje wówczas 7 rzędów po 7 kolumn (po wykreśleniu rzędu i kolumny, w których stoi już pierwsza wieża), dla trzeciej analogicznie 6×6 i dla czwartej - 5×5. Mamy więc 64?49?36?25 możliwych ustawień kolejno czterech wież. Figury szachowe są jednak nierozróżnialne, więc zamiana np. wieży pierwszej z czwartą nie zmienia układu na szachownicy. Ogólnie wszystkie możliwe ustawienia wież różniące się tylko kolejnościa ich stawiania dają taki sam układ. Możliwych ustaleń kolejności czterech elementów (tzw. permutacji) jest 4·3·2·1 (pierwszy można wybrać na 4 sposoby, drugi na 3 itd.), a otrzymaną poprzednio liczbę trzeba więc przez tyle podzielić. Odpowiedzią jest zatem 64·49·36·25/4·3·2·1=117600.
Zad. 2. Liczbami pierwszymi, które są numerami miesięcy lub dni miesięcy, są 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Tylko ich sumy zawierające 2 jako jeden ze składników mogą być liczbami pierwszymi, bo wszystkie pozostałe są parzyste i większe od 2. Spośród nich tylko 2+3, 2+5, 2+11, 2+17 i 2+29 są rzeczywiście pierwsze. Wszystkie dają odpowiednie daty w lutym (3, 5, 11, 17 i 29 - 2008 jest rokiem przestępnym), a pierwsze trzy dają drugie dni trzech miesięcy (III, V i XI). W sumie jest więc 8 takich dat.
Zad. 3. Kolejne odcinki pokonywane przez Kleofasa mają długości 1, 1, 2, 2, 3, 3, ... [cm]. Gdy przebędzie ich 2n, pokona w sumie drogę 1+n + 2+(n-1) + 3+(n-2) + ... + (n-1)+2 + n+1 [cm]. Po wygodnym pogrupowaniu składników sumy daje to (n+1)·n. Łatwo sprawdzić, że dla n=44 daje to 1980, więc 2008. cm Kleofas pokona jako 28. cm pierwszego przebieganego odcinka długości 45 cm. Odcinek ten leży pionowo na lewo od punktu startu Kleofasa i jego dolny koniec (przez który Kleofas pojawi się na tym odcinku) jest o 22 cm w lewo i 22 cm w dół od punktu startu (bo dolny koniec pierwszego odcinka długości 1 cm leży o 0 cm w lewo i 0 cm w dół od punktu startu, dolny koniec pierwszego odcinka długości 3 cm - o 1 cm w lewo i 1 cm w dół itd. - dolny koniec pierwszego odcinka długości (2n+1) cm leży o n cm w lewo i n cm w dół). Kleofas będzie więc o 22 cm w lewo i 6 cm w górę od punktu startu, czyli w odległości (222+62) = 2·130 cm od niego.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
