Zad. 1. Udowodnij, że dla n naturalnych liczba 49n·(49n+1)+1 jest złożona.
Zad. 2. Znajdź liczbę naturalną n, dla której liczby 5n−4 i 5n+4 są parzyste.
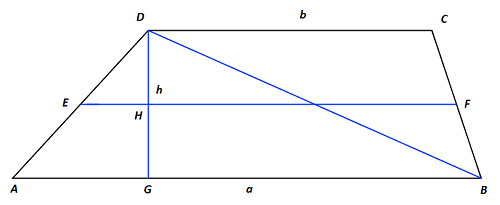
Zad. 3. Trapez ABCD podzielono na części odcinkiem łączącym środki nierównoległych boków. Powstałe w ten sposób figury mają pola równe 9 cm2 i 4 cm2. Ile wynoszą pola figur, na które dzieli ten trapez jego przekątna?
W tym miesiącu punkty zdobyli:
- 3 pkt. - Kacper Gembara G w ZSS Wołów, Oliwia Kropidłowska G 1 Wrocław, Konrad Litwiński G 86 Warszawa, Zofia Ogonek G 58 Warszawa, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński, Mateusz Rzepecki G 14 Wrocław i Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski,
- 2,5 pkt. - Aleksandra Domagała G 23 Wrocław, Joanna Lisiowska KZE Warszawa, Magdalena Owczarek G Dwujęzyczne Legionowo, Łukasz Pawlak G Dwijęzyczne Oborniki Śląskie i Krzysztof Żmuda G Wieczfnia Kościelna,
- 2 pkt. - Iwo Pilecki-Silva G 26 Wrocław,
- 1 pkt. - Helena John G Wielowieś.
Pozostali uczestnicy zdobyli poniżej 1 punktu.
Po czterech miesiącach Ligi Zadaniowej z wynikiem 12 pkt. (na 12 możliwych) prowadzą: Konrad Litwiński, Mateusz Rzepecki i Michał Stempniak. Drugie miejsce z wynikiem 11 pkt. zajmują: Kacper Gembara, Oliwia Kropidłowska i Zofia Ogonek. Trzecie miejsce z wynikiem 10 pkt. zajmują: Joanna Lisiowska i Krzysztof Żmuda. Gratulujemy!
Zad. 1. Zauważmy, że 49n·(49n+1)+1=(72n+1)2-72n=(72n+1-7n)·(72n+1+7n).
A ponieważ dla n≥1 liczby (72n+1-7n) i (72n+1+7n) są różne od 1 i od 49n·(49n+1)+1,
więc liczba 49n·(49n+1)+1 jest złożona dla dowolnego n naturalnego.
Zad. 2. Liczba 5n dla n naturalnych jest nieparzysta, ponieważ jej cyfra jedności to 5. A ponieważ suma i różnica liczby nieparzystej i parzystej jest zawsze nieparzysta, to liczby 5n−4 i 5n+4 są nieparzyste dla dowolnego n naturalnego.
Zad. 3. Oznaczmy |AB|=a, |CD|=b i |DG|=h. Łącząc środki nierównoległych boków trapezu ABCD, uzyskamy dwa trapezy ABEF i CDEF. Ich pola to odpowiednio 9 cm2 i 4 cm2. Stąd dostajemy dwa równania (a+(a+b)/2)·h/4=9 i (b+(a+b)/2)·h/4=4. Rozwiązując układ tych równań, obliczamy, że a·h=23 i b·h=3. Stąd pola trójkątów ABD i BCD są równe odpowiednio a·h/2=11,5 cm2 i b·h/2=1,5 cm2. Na koniec zauważmy, że wybór przekątnej trapezu ABCD nie ma znaczenia, bo obie dzielą ten trapez na dwa trójkąty o polach 11,5 cm2 i 1,5 cm2.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
