Zad. 1. Udowodnij, że dla każdych trzech liczb całkowitych dodatnich, suma dwóch z nich jest parzysta.
Zad. 2. Niech x>y>0, oraz 6x2 + 6y2 = 13xy. Jaką wartość ma wyrażenie (x+y)/(x-y)?
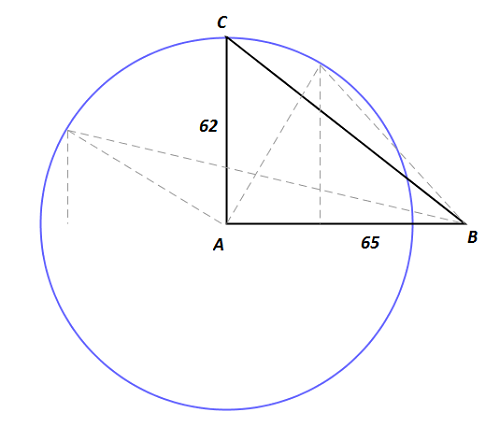
Zad. 3. Udowodnij, że pole trójkąta o bokach długości 62 i 65 nie może być większe od 2015.
W tym miesiącu punkty zdobyli:
- 3 pkt. - Aleksandra Domagała G 23 Wrocław, Kacper Gembara G w ZSS Wołów, Joanna Lisiowska KZE Warszawa, Konrad Litwiński G 86 Warszawa, Łukasz Pawlak G Dwujęzyczne Oborniki Śląskie, Przemysław Rybarczyk G Integracyjne Stargard Szczeciński, Mateusz Rzepecki G 14 Wrocław, Michał Stempniak G Sióstr Salezjanek Ostrów Wielkopolski i Krzysztof Żmuda G Wieczfnia Kościelna,
- 2,5 pkt. - Oliwia Kropidłowska G 1 Wrocław i Zofia Ogonek G 58 Warszawa,
- 2 pkt. - Magdalena Owczarek G Dwijęzyczne Legionowo i Iwo Pilecki-Silva G 26 Wrocław,
- 0,5 pkt. - Helena John G Wielowieś.
Pozostali uczestnicy zdobyli poniżej 0,5 punktu.
Po pięciu miesiącach Ligi Zadaniowej z wynikiem 15 pkt. (na 15 możliwych) prowadzą: Konrad Litwiński, Mateusz Rzepecki i Michał Stempniak. Drugie miejsce z wynikiem 14 pkt. zajmuje: Kacper Gembara. Trzecie miejsce z wynikiem 13,5 pkt. zajmują: Oliwia Kropidłowska i Zofia Ogonek. Gratulujemy!
Zad. 1. Dla dowolnych trzech liczb całkowitych dodatnich może zajść jeden z przypadków: albo co najmniej dwie liczby spośród z nich są parzyste, albo co najmniej dwie są nieparzyste. Suma dwóch liczb parzystych jest parzysta podobnie jak suma dwóch liczb nieparzystych. Udowodniliśmy więc, że wśród dowolnych trzech liczb całkowitych dodatnich istnieją dwie, których suma jest liczba parzystą.
Zad. 2. Wyrażenie ma wartość 5. Zauważmy, że równanie 6x2 + 6y2 = 13xy można przekształcić do postaci 6x2-4xy+6y2-9xy = 0 i dalej 2x(3x-2y) - 3y(3x-2y) = 0, a w końcu (3x-2y)(2x-3y) = 0. Ponieważ x>y>0, musi być x=1,5y. Podstawiając to do wyjściowego wyrażenia, dostajemy (x+y)/(x-y)=5.
Zad. 3. Przy ustalonych długościach dwóch boków trójkąt ma największe pole, jeśli te boki są przyprostokątnymi w trójkącie prostokątnym. Wtedy pole trójkąta o danych bokach wynosi 0,5·65·62 = 2015. Bez zmniejszenie ogólności przyjmijmy, że podstawa AB trójkąta ABC ma długość 65. Pole trójkąta jest iloczynem połowy długości podstawy i wysokości, a wysokość jest największa, gdy jest równa drugiemu danemu bokowi, czyli dane boki są przyprostokątnymi trójkąta prostokątnego.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
