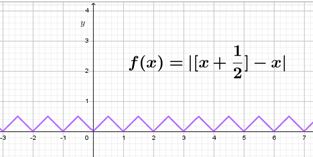
Zad. 1. Naszkicuj wykres funkcji f (x) = |[x + 1/2]− x|, gdzie [a] oznacza część całkowitą liczby rzeczywistej a.
Zad. 2. Na jaką największą liczbę części prosta może rozciąć wielokąt o 2018 wierzchołkach?
Zad. 3. Sklejono ścianami trójkątnymi czworościan foremny o krawędzi a i ostrosłup czworokątny, którego wszystkie krawędzie mają długość a. Ile ścian, wierzchołków i krawędzi ma otrzymany wielościan?
W styczniu punkty zdobyli:
• 3 pkt. – Bartłomiej Zug LO Oleśno, Jakub Dobrzański LO I Lubin,
• 2 pkt. – Joanna Lisiowska XXI LO Warszawa, Bartosz Matysiak LO Kalisz
• 1 pkt.– Zuzanna Szymańska VIII LO Wrocław,
• 0,5 pkt. – Mikołaj Zapotoczny LO Ząbkowice Śl.
Po czterech miesiącach Ligi Zadaniowej dla LO prowadzą:
- I m. (z wynikiem 11 pkt. na 12 możliwych) – Joanna Lisiowska,
- II m.(z wynikiem 9,5 pkt.) – Jakub Dobrzański,
- III m. (z wynikiem 8,5 pkt.) – Bartłomiej Zug.
Gratulujemy!
Zad. 1. Wykres przedstawiono na poniższym rysunku.
Zad. 2. Wielokąt o 2018 wierzchołkach można rozciąć prostą na 2018:2+1 =1010 części, jak pokazano na rysunku.
Zad. 3. Wierzchołek czworościanu leży na prostej będącej częścią wspólną płaszczyzn zawierających przeciwległe ściany boczne ostrosłupa kwadratowego (dlaczego?). Otrzymany wielościan ma więc 5 ścian (dwie w kształcie rombu, jedną kwadratową i dwie trójkątne), 6 wierzchołków i 9 krawędzi.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
