Zad. 1. Odpowiedz na pytania:
a) Czym są i do czego służą CP620(CP790) i Windows-1250?
b) Co mają wspólnego, a czym się różnią?
c) Na podstwie czego powstał CP790 i czym się różni od pierwowzoru?
Zad. 2. Podaj rozwiązania łamigłówek RoboZZle.
a) łamigłówka nr 1
b) łamigłówka nr 2
W jakim zakresie można zoptymalizować rozwiązanie? Zoptymalizowane rozwiązanie będzie dodatkowo premiowane :)
Zad. 3. Rozwiąż poniższy algebraf. Litery są przyporządkowane wzajemnie jednoznacznie cyfrom. Żadna liczba nie zaczyna się zerem. Uzasadnij, że znalazłeś wszystkie rozwiązania.
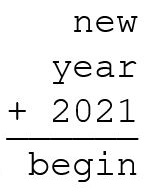
Zadania noworoczne okazały się całkiem proste. Drobne problemy sprawiło wyznaczenie wzystkich rozwiązań algebrafu. Za to większość zawodników zoptymalizowała rozwiązania łamigłówek.
Punkty zdobyli:
- 4 pkt. - Krystyna Lisiowska - redaktor z Warszawy, Andrzej Piasecki - administrator IT z Oleśnicy,
- 3 pkt. - Igor Wojtun - uczeń I LO w Głogowie,
- 2,5 pkt. - Krzysztof Danielak - student data science na UE we Wrocławiu.
Po czterech miesiącach trwania Ligi zawodnicy zdobyli dotychczas następujące liczby punktów:
- 11,5 pkt. - Krystyna Lisiowska - redaktor z Warszawy, Andrzej Piasecki - administrator IT z Oleśnicy,
- 9,5 pkt. - Igor Wojtun - uczeń I LO w Głogowie,
- 6,25 pkt. - Krzysztof Danielak - student data science na UE we Wrocławiu,
- 1,25 pkt. - Dominik Zygmunt - ekonomista z Białej Rawskiej.
Zad. 1.
a) CP620 i Windows-1250 to strony kodowania, czyli zestawy podswtaowych znaków wykorzystywanych w komputerach do obsługi danego języka.
b) Najlepiej to obrazują poniższe zdjęcia.
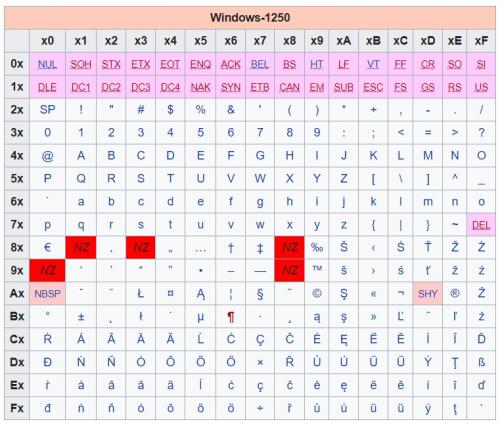
CP790:
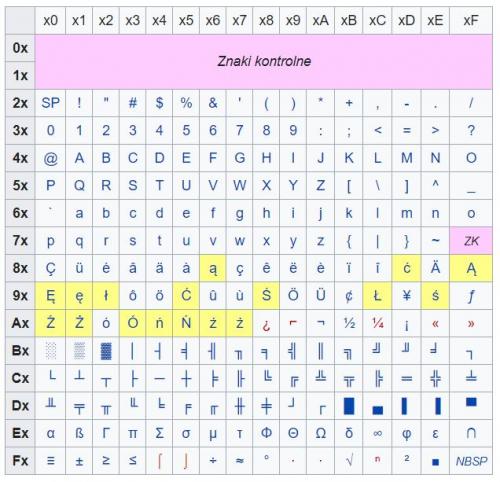
c) CP790 powstał na bazie CP437, a różnice przedstawiają żółte pola na powyższysz zdjęciu.
Zad. 2. Możliwe rozwiązania (a i b)
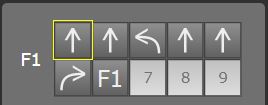
Rozwiązanie można zoptymalizować pod względem dwóch aspektów: liczby komend oraz liczby wykonań. Rozwiązanie rozgrywki b jest zoptymalizowane pod względem liczby komend, ale w tym przypadku za cenę dwukrotnego przechodzenia przez wewnętrzne pola.
Zad. 3. Ten alegbraf ma 4 rozwiązania:
a) 307 + 8095 + 2021 = 10423
b) 305 + 8097 + 2021 = 10423
c) 406 + 8097 + 2021 = 10524
d) 407 + 8096 + 2021 = 10524
Uzasadnienie. Zauważmy, że y+2 = be. Jeśli y=8, to be=10, jeśli y=9, to be=11, ale nie może zajść b=e=1, zatem y=8, b=1, e=0. Wtedy n+e+0 = g, a ponieważ e=0, to n=g, co nie może zajść, zatem mamy przeniesienie 10 z e+a+2, czyli n+1=g, a=9 (bo 8 już zajęte przez y). Wtedy powinno być i=1, co też nie może zajść, bo już b=1, zatem mamy kolejne przeniesienie 10 z w+r+1=n, czyli i=2. Niewykorzystane cyfry to 3, 4, 5, 6 i 7. Mamy n+1=g oraz w+r+1=n > 12, bo i=2. Pary (w, r) ze zbioru {(3, 4), (3, 5), (3, 6), (3, 7), (4, 5), (4, 6), (4, 7), (5, 6)} odpadają, bo wtedy suma w+r+1 nie przekroczy 12. Zatem albo w=5 i r=7 lub w=7 i r=5, a wtedy 5+7+1=13 i n=3, g=4, albo w=6 i r=7 lub w=7 i r=6, a wtedy 6+7+1=14 i n=4, g=5.
Jest jeszcze możliwość, w której n+e+0 jest większe od 10 lub równe 10. Wtedy y+2+1=be, czyli y=8 i b=e=1 (co nie spełnia warunku algebrafu) lub y=9, b=1 i e=2. Dalej n+e+0=g, zatem n+2=g >9, czyli n=8, g=0. Dalej e+a+2 <10, bo inaczej byłoby g=b=1. Zatem a+4=i <10 oraz w+r+1=8, czyli w+r=7. Wolne cyfry to 3, 4, 5, 6 i 7. Zatem w=3 i r=4 lub w=4 i r=3. Niewykorzystane cyfry to 5, 6 i 7, ale wtedy a+4=i, czyli i–a=4, a różnica najwiekszej cyfry z najmniejszą wynosi 7-5=2. co implikuje, że przeniesienie nie zachodzi.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
