Zad. 1. Rozwiąż klasyczne sudoku. Wyniki podaj kolejnymi wierszami.
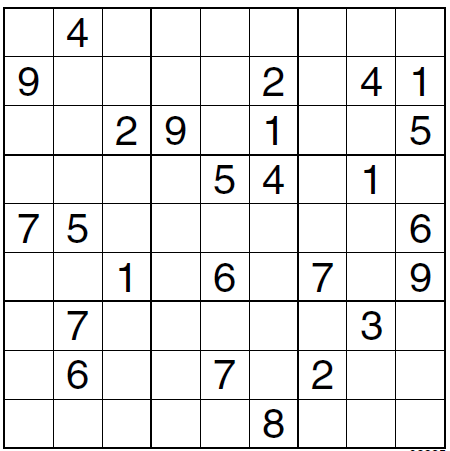
Zad. 2. Ponumeruj płytki liczbami od 1 do 4 tak, aby płytki z tym samym numerem nie stykały się ani fragmentem boku, ani wierzchołkiem.
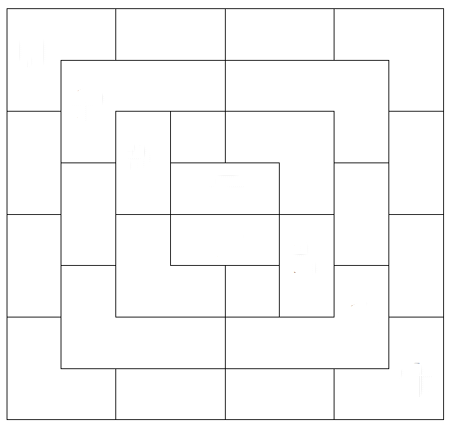
Zad. 3. Jaka jest największa liczba naturalna n taka, że 10n dzieli 2023!?
W tym miesiącu punkty otrzymali:
- 3 pkt. - Daria Bumażnik - doktorantka na WCh UWr, Agata Leśnicka - lekarz z Gdańska, Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Edward Nowicki - informatyk z Poznania, Kasper Przenzak - analityk ryzyka z Krakowa, Tomasz Tomiczek - nauczyciel z Lipowej, Marzena Wąsiewicz - nauczycielka z Kajetan, Michał Węgrzyn - ALO PWr Wrocław, Dominik Zygmunt - specjalista ds. administrowania wierzytelnościami z Białej Rawskiej,
- 2 pkt. - Joanna Miłkowska - pracownik biurowy ze Stalowej Woli, Dąbrówka Mocha - kontroler finansowy z Wrocławia.
Zad. 1. Rozwiązanie przedstawia diagram.
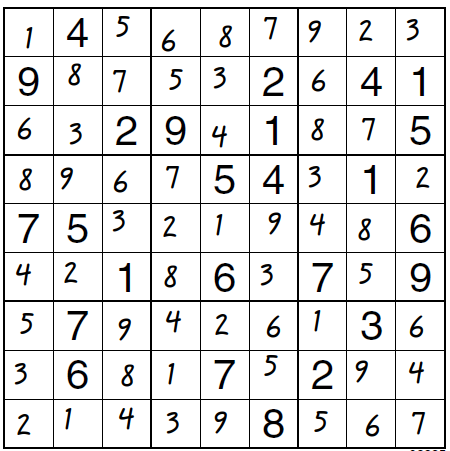
Zad. 2. Przykładowe rozwiązanie przedstawia diagram.
Zad. 3. Innymi słowy pytanie z zadania brzmi: iloma zerami kończy się 2023!. Tych zer jest tyle, ile razy można tę liczbę podzielić bez reszty przez 10 (dlaczego?), a w przypadku silni oznacza to tosamo, co podzielić liczbę bez reszty przez 5 (bo dwójek w silni, które uzupełnią piątki do dziesiątek jest wystarczająco dużo - dlaczego?). W liczbie 2023! co piąty składnik dzieli się przez 5, co 25 - dzieli się przez 5 dwukrotnie, co 125 - trzykrotnie i co 625 - czterokrotnie. Zatem podzielność przez 5 zachodzi [2023/5]+[2023/25]+[2023/125]+[2023/625] = 404+80+16+3 = 503 razy, gdzie symbol [.] oznacza część całkowitą liczby. Największe możliwe n to 503.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
