- Mysterium Cosmographicum - 1596
- Ad Vitellionem paralipomena - 1604
- De stella nova - 1604
- Astronomia nova - 1609
- Dioptrices - 1611
- Nova stereometria doliorum viniarorum - 1615
- Epitomes astronomiae Copernicanae - 1617, 1621
- Harmonices mundi - 1619
- Tabulae Rudolfinae - 1627
- Somnium seu opus posthumum de astronomia lunari - 1634
Matematyk, fizyk i astronom. Urodził się w 1571 roku w Weil der Stadt pod Stuttgartem jako najstarszy syn oficera armii niemieckiej. Studiował w Tybindze, gdzie szczególny wpływ wywarły na niego nauki Michała Mastlina, który w odróżnieniu od większości ówczesnych uczonych, był gorącym zwolennikiem heliocentrycznej teorii Kopernika. Po opuszczeniu Tybingi przez kilka lat uczył matematyki i astronomii w seminarium protestanckim w Grazu w Austrii. W tym czasie powstała jego pierwsza książka z astronomii - "Mysterium Cosmographicum" (Tajemnica kosmograficzna), jednak teoria, którą w niej przedstawił, okazała się całkowicie błędna, do czego doszedł w swoich dalszych badaniach.
Z Grazu musiał uciekać przed prześladowaniami religijnymi i w 1600 roku przeniósł się do Pragi, gdzie został współpracownikiem Tychona Brahego - nadwornego astronoma cesarza Austrii - Rudolfa II. Po tragicznej śmierci Brahego w 1601 roku, to właśnie Kepler objął stanowisko nadwornego astronoma Habsburgów. Brahe przekazał mu obszerny zbiór niezwykle precyzyjnych obserwacji planet, które przez wiele lat prowadził w swoim wspaniale wyposażonym obserwatorium Uraniborg na duńskiej wyspie Hven. To dzięki tym notatkom Kepler sformułował cztery prawa ruchu planet. Trzech z nich do dziś uczymy się w szkole. Czwarte według współczesnej metodologii naukowej nie znalazło poparcia teoretycznego i obecnie nie jest uznawane za prawo przyrody, a jedynie za ciekawą zbieżność.
Pierwsze i drugie prawo ruchu planet wokół Słońca opublikował Kepler w roku 1609 w dziele "Astronomia nova", a trzecie w dziele "Harmonices mundi" (Harmonia świata), napisanym w Linzu (Austria), gdzie przebywał jako wykładowca matematyki w latach 1612-1626. Tzw. czwarte prawo Keplera znajdziemy we wspomnianej już debiutanckiej książce (opublikowanej w 1596 roku) - "Mysterium cosmographicum".
Od roku 1626 Kepler mieszkał w Ulm (Niemcy), gdzie w 1627 roku opublikował słynne tablice ruchu planet "Tabulae Rudolfinae" (Tablice rudolfińskie - nazwane tak na cześć jego protektora i sponsora - cesarza Rudolfa II), które dla wielu pokoleń astronomów były niedoścignionym wzorem precyzji i nieocenioną pomocą w pracach obserwacyjnych.
W 1628 roku Kepler przeniósł się do Żagania, dokąd zaprosił go książę Albrecht Wallenstein. Przebywał tam niemal do samej śmierci. Zmarł 15 XI 1630 roku w Regensburgu. Dla upamiętnienia pobytu i działalności Keplera w Żaganiu w latach 1628-1630 w rocznicę jego śmierci w 2000 roku odsłonięto w parku miejskim pamiątkowy medalion z jego podobizną. Na Rynku z Żaganiu stoi też pomnik Keplera. Ten i wiele innych wystawionych mu w różnych miastach pomników można zobaczyć tutaj.
- Trzy prawa Keplera opisujące ruch planet wokół Słońca
I. Ruch każdej planety odbywa się po elipsie, zaś Słońce znajduje się w jednym z jej ognisk.
II. Promień wodzący planety zakreśla w równych odstępach czasu równe pola (tzw. prawo pól).
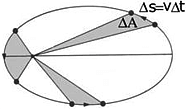
III. Kwadraty okresów obiegów planet dookoła Słońca (T1, T2) są wprost proporcjonalne do sześcianów ich średnich odległości od Słońca (a1, a2).
[tex]\frac{T_1^2}{T_2^2} = \frac{a_1^3}{a_2^3}[/tex]
Dziś trzy prawa Keplera traktujemy jako wnioski wynikające z prawa powszechnego ciążenia odkrytego przez Izaaka Newtona.
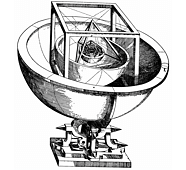Czwarte prawo Keplera: jeśli na sferze wyznaczonej przez orbitę Merkurego opiszemy ośmiościan foremny, to okaże się, że jest on wpisany w sferę Wenus. Jeśli na sferze Wenus opiszemy dwudziestościan foremny, to będzie on wpisany w sferę Ziemi. Dwunastościan foremny opisany na tej sferze jest wpisany w sferę Marsa, a czworościan foremny opisany na sferze Marsa jest wpisany w sferę Jowisza. Z kolei sześcian opisany na sferze Jowisza jest wpisany w sferę Saturna. W ten sposób odkryta została liczbowa harmonia w Układzie Słonecznym.
Precyzyjne obliczenie obszernych tablic ruchu planet opartych na prawach Keplera (opublikowanie wyników w Tablicach rudolfińskich).
- Wprowadzenie układu współrzędnych biegunowych, w którym obiera się punkt (0, 0) zwany biegunem i wychodzącą z niego półprostą zwaną osią biegunową). Następnie każdemu punktowi płaszczyzny przyporządkowuje się parę liczb złożoną z odległości tego punktu od bieguna i kąta, jaki promień wodzący punktu wyprowadzony z bieguna tworzy z osią biegunową.
- Propozycja atomistycznej teorii figur geometrycznych, która zakłada, że mogą one być rozbite na nieskończenie wiele niepodzielnych jednostek (linie złożone są z punktów, powierzchnie z linii, a bryły z powierzchni, sfera to suma stożków, a stożek to suma trójkątów itd.)
- Wprowadzenie po raz pierwszy do geometrii wielkości nieskończenie małych i nieskończenie dużych.
- Udział w badaniach, które doprowadziły Newtona do odkrycia rachunku różniczkowego i całkowego. W pracy "Nova stereometria doliorum viniarorum" Kepler zajął się m. in. problemem wyznaczania objętości beczek z winem, co doprowadziło go do rozważania powierzchni ich przekrojów oraz do wyznaczania minimów i maksimów. Innym problemem, który pojawił się w tym dziele, był odwrotny problem stycznych. Polegał on na odtworzeniu krzywej, jeśli znane były styczne do niej w każdym punkcie (co stanowi w rachunku różniczkowym standardowy problemem obliczania całki).
- Badanie problemu rektyfikacji, czyli obliczania długości krzywych. Rektyfikacja krzywej jest to zadanie konstrukcyjne polegające na wykreśleniu (za pomocą cyrkla i linijki bez podziałki) odcinka o długości równej długości zadanego łuku rozważanej krzywej.
Wynalazek lunety zbudowanej z dwóch soczewek skupiających.- Wprowadzenie przecinka do notacji ułamków dziesiętnych.
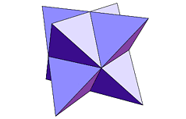
- Opis matematycznych własności wielościanu gwiaździstego zwanego stella octangula (gwiazda ośmioramienna), którą opisał w 1609 roku.
- Pierwszy w czasach nowożytnych opis wszystkich istniejących wielościanów archimedesowych (w "Harmonices Mundi" - 1619) oraz dwóch z czterech wielościanów gwiaździstych nieforemnych. Dziś wiadomo, że oprócz pięciu foremnych wielościanów wypukłych istnieją jeszcze cztery niewypukłe, które noszą nazwę wielościanów Keplera-Poinsota. Matematyczne własności dwóch z nich - dwunastościanu gwiaździstego małego i dużego jako pierwszy opisał Kepler.
- Kepler napisał wiele książek i listów, w których wyjaśniał szczegółowo swoje odkrycia. Przedstawiał w nich zarówno braki jak i zalety tych odkryć.
- Kepler, tak jak Pitagorejczycy, szukał w matematyce sposobu rozumienia świata. Świadczą o tym tytuły jego dzieł: Mysterium Cosmographicum lub Harmonices mundi. W tym ostatnim można także zauważyć wpływ Pitagorasa, który uważał, że każda planeta w swojej wędrówce po orbicie wydaje przyjemne dźwięki, których jednak nie słyszymy (stąd pochodzi zwrot "harmonia sfer"). Kepler rozwinął ten pogląd. Uważał, że "muzyka niebios" jest ciągła, wielogłosowa, a usłyszeć ją można tylko intelektem.
- Kepler jest autorem książki, Somnium seu opus posthumum de astronomia lunari (Sen lub astronomia księżycowa) uznawanej za pierwowzór literatury fantastyczno-naukowej. Rozmyśla w niej o tym, co można zobaczyć po wylądowaniu na Księżycu, jak z Księżyca wygląda Ziemia i jak usytuowane są gwiazdy. Prace nad tą książką Kepler rozpoczął jeszcze na studiach w Tybindze, a zakończył w Żaganiu. W rocznicę śmierci Keplera 15 XI 2004 roku ukazał się polski przekład jego opowieści o podróży na Księżyc z obszernym komentarzem.
- Kepler nazywał liczby niewymierne "niewypowiedzianymi".
- Oprócz działalności badawczej Kepler zajmował się (jak każdy ówczesny nadworny astronom) stawianiem horoskopów władcy. Ogromną sławę przyniósł mu horoskop sporządzony dla księcia Albrechta Wallensteina, w którym przewidział datę jego śmierci. Przepowiednia ta sprawdziła się podobno co do dnia.
- O znaczeniu odkryć Keplera i uznaniu, jakim cieszy się na całym świecie, świadczą wydawane w różnych krajach znaczki pocztowe z jego podobizną
- Bóg jest matematykiem.
- Moim przekonaniem jest, że okoliczności, w jakich ludzie zdobywają wiedzę o zjawiskach niebieskich, są nie mniej warte niż same odkrycia.
- A były głównie trzy problemy, których przyczyn, dlaczego jest tak, a nie inaczej, szukałem. A były to liczba, wielkość i ruch sfer. Odwagi dodała mi owa idealna zgodność pozostających w bezruchu Słońca, gwiazd stałych i przestrzeni pośredniej z Bogiem-Ojcem, Synem i Duchem Świętym.
- Geometria istniała przed Stworzeniem, jest zatem równie nieśmiertelna, co i duch Boży. Jest samym Bogiem.
- Kości zostały rzucone, książka jest napisana i jest mi obojętne czy będzie czytana teraz, czy w przyszłości. Może czekać przez sto lat na czytelnika, jak Bóg czekał sześć tysięcy lat na obserwatora.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
