stopień trudności:
- podwyższony, sprawdzian przeznaczony dla klas z rozszerzonymi treściami z matematyki
- zadanie z (*) jest obowiązkowe na ocenę celującą
- grupy A i B mają ten sam poziom
ocenianie:
19-20 - celujący
16-19 - bardzo dobry
13-15 - dobry
10-12 - dostateczny
6-9 - dopuszczający
0-5 - niedostateczny
czas pisania: 45 minut
typ sprawdzianu:
Sprawdzający wiadomości po zakończeniu działu tematycznego lub powtarzający wiadomości z danego działu przed testem kompetencji. Zadania traktujemy jako otwarte, uczeń powinien przedstawić pełny tok rozumowania i obliczenia.
Grupa A (20 pkt)
Zad. 1. (4 pkt ) Proste k i l są równoległe. Oblicz długości odcinków: a) x, b) y.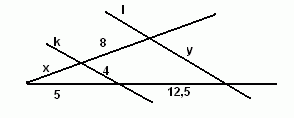
Zad. 2. (2 pkt) Trójkąty ABC i KLM są podobne, |AB| = 9 cm, |BC| = 12 cm, |AC| = 15 cm.
Znajdź długości boków trójkąta KLM, wiedząc, że jego najdłuższy bok ma 12 cm. Wyznacz skalę podobieństwa [tex]\triangle[/tex]ABC do [tex]\triangle[/tex]KLM.
Zad. 3. (3 pkt) Dany jest prostokąt ABCD o bokach długości 3 cm i 8 cm oraz podobny do niego prostokąt A'B'C'D' o obwodzie 6 cm. Oblicz długości boków prostokąta A'B'C'D'.
Zad. 4. (3 pkt) Pole trójkąta ABC jest równe 12 cm2. Oblicz pole podobnego do niego trójkąta A'B'C', wiedząc, że jego obwód jest dwa razy większy od obwodu trójkąta ABC. Podaj skalę podobieństwa tych trójkątów.
Zad. 5. (3 pkt) Maszt anteny telefonii komórkowej rzuca cień długości 15 m. W tym samym czasie cień rosnącego nieopodal pionowego drzewa, którego wysokość jest równa 12 m, ma długość 10 m. Oblicz wysokość masztu.
Zad. 6. (3 pkt) Wafel w kształcie trójkąta równoramiennego ma podstawę długości 8 cm i opuszczoną na nią wysokość długości 6 cm. Mama przekroiła go jednym cięciem noża równolegle do podstawy, tak że linia cięcia ma 4,8 cm. Część trójkątną dostał Jacek, a czworokątną Placek. Czy ten podział był sprawiedliwy? Jeśli nie, to jaką część wafla dostał każdy z chłopców? W jakiej odległości od wierzchołka powinno wypaść cięcie, aby podział był sprawiedliwy?
Zad. 7*. (2 pkt) W trójkąt równoboczny ABC o boku a = 6 cm wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe dwa na bokach trójkąta. Oblicz długość boku kwadratu.
Grupa B (20 pkt)
Zad. 1. (4 pkt) Proste k i l są równoległe. Oblicz długości odcinków: a) x, b) y.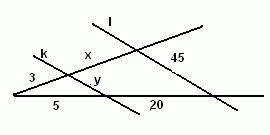
Zad. 2. (2 pkt) Trójkąty ABC i EFG są podobne, |AB| = 6 cm, |BC| = 8cm, |AC| = 10 cm. Znajdź długości boków trójkąta EFG, wiedząc, że jego najkrótszy bok ma 4 cm. Wyznacz skalę podobieństwa [tex]\triangle[/tex]EFG do [tex]\triangle[/tex]ABC.
Zad. 3. (3 pkt) Dany jest prostokąt ABCD o bokach długości 6 cm i 12 cm oraz podobny do niego prostokąt A'B'C'D' o obwodzie 8 cm. Oblicz długości boków prostokąta A'B'C'D'.
Zad. 4. (3 pkt) Pole trójkąta KLM jest równe 15 cm2. Oblicz pole podobnego do niego trójkąta K'L'M', wiedząc, że jego obwód jest 3 razy większy od obwodu trójkąta KLM. Podaj skalę podobieństwa tych trójkątów.
Zad. 5. (3 pkt) Maszt anteny telefonii komórkowej o wysokości 9 m rzuca cień o długości 12 m. W tym samym czasie cień rosnącego obok pionowego drzewa ma długość 6 m. Oblicz wysokość drzewa.
Zad. 6. (3 pkt) Park pałacowy ma kształt trapezu równoramiennego. Jego krótsza podstawa ma 8 jardów, ramię 13 jardów, a wysokość 12 jardów. Królewski ogrodnik postanowił zwiększyć powierzchnię parku, dodając obszar ograniczony przedłużeniami ramion trapezu aż do punktu ich przecięcia. Jaki obwód i jakie pole powierzchni będzie miał powiększony park?
Zad. 7*. (2 pkt) W trójkąt równoboczny EFG o boku c = 4 cm wpisano kwadrat w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe dwa na bokach trójkąta. Oblicz długość boku kwadratu.
odpowiedzi:
grupa A
1. a) 3,2 b) 14
2. skala podobieństwa = 1,25, długości boków: 7,2 cm, 9,6 cm
3. [tex]\frac{9}{11}[/tex]cm, 2
4. pole = 48 cm2, skala podobieństwa = 2
5. 18 m
6. nie, Jacek - 0,36 Placek - 0,64 wafla, 3√2 cm
7. (12√3 - 18) cm
grupa B
1. a) 12 b) 9
2. skala podobieństwa = [tex]\frac{2}{3}[/tex], długości boków: 5[tex]\frac{1}{3}[/tex] cm, 6[tex]\frac{2}{3}[/tex] cm
3. 1[tex]\frac{1}{3}[/tex] cm, 2[tex]\frac{2}{3}[/tex] cm
4. pole = 135 cm2, skala podobieństwa = 3
5. 4,5 m
6. 64,8 jarda, 156 jardów kwadratowych
7. (8√3 - 12) cm
kryteria oceniania
1. a)-b) 1 pkt za proporcję, 1 pkt za odpowiedź z uzasadnieniem proporcji
2. 1 pkt za obliczenie skali podobieństwa,1 pkt za podanie obliczenie długości boków
3. 1 pkt za ułożenie układu równań, 1 pkt za wyliczenie długości boków, 1 pkt za wynik z jednostką
4. 1 pkt za podanie skali podobieństwa, 1 pkt za stosunek pól, 1 pkt za wynik z jednostką
5. 1 pkt za rysunek i wskazanie trójkątów podobnych (lub powołanie się na tw. Talesa, 1 pkt za ustalenie poprawnej proporcji, 1 pkt za odpowiedź
6. gr A. 1 pkt za obliczenie skali podobieństwa odciętego trójkąta do wyjściowego, 1 pkt za obliczenie, jaką część dostał każdy z chłopców, 1 pkt za obliczenie odległości cięcia
6. gr B. 0,5 pkt za obliczenie długości dolnej podstawy, 1 pkt za uzasadnienie podobieństwa dodanego obszaru do całości i podanie skali, 0,5 pkt za obliczenie długości ramienia dodanego trójkąta, 0,5 pkt za obliczenie pola całego obszaru, 0,5 pkt za podanie odpowiedzi
7. 1 pkt za proporcję z uzasadnieniem, 1 pkt za wyznaczenie długości boku kwadratu
