Każda liczba naturalna jest równa swojemu podwojeniu
Niech x przyjmuje wartości naturalne, wtedy
x + x + ... + x = x2 /dx (po lewej stronie x występuje x razy)
1 + 1 + ... + 1 = 2x (po lewej stronie 1 występuje x razy)
x = 2x dla każdego x naturalnego.
***
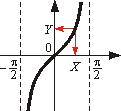Prosta i odcinek bez końców mają tyle samo punktów
Punkty prostej i punkty odcinka można ustawić w pary, tak że żaden nie pozostanie bez pary. Oznacza to, że punktów jest tyle samo na prostej, co na odcinku. Takie ustawienie w pary wyznacza np. funkcja y = tgx (patrz rysunek obok).
***
Funkcja rosnąca może mieć ujemną pochodną
Iloczyn funkcji rosnących jest funkcją rosnącą.
Funkcje x-1, x-2, x-3 są wszystkie rosnące (bo pochodna każdej z nich jest równa 1).
Stąd f(x) = (x-1)(x-2)(x-3) = x3 - 6x2 + 11x - 6 jest rosnąca.
Pochodna f '(x) = 3x2 - 12x + 11 jest więc zawsze dodatnia.
Ale f '(2) = 12 - 24 + 11 = -1.
***
1 nie jest granicą ciągu 1-1/n
Załóżmy nie wprost, że
$$\lim_{n \to\infty}\left(1-\frac{1}{n}\right)=1.$$
Wtedy z definicji
$$(\forall\varepsilon>0)(\exists k\in \mbox{I} \! \mbox{N})(\forall n > k)\left(\left|\left(1-\frac{1}{n}\right)-1\right|<\varepsilon\right)$$
gdzie $ \mbox{I} \! \mbox{N}$ oznacza zbiór liczb naturalnych.
Mamy
$$\left| 1-\frac{1}{n}-1\right|< \varepsilon$$
$$\Downarrow$$
$$\left| -\frac{1}{n}\right|< \varepsilon$$
$$\Downarrow$$
$$\frac{1}{n}< \varepsilon\ \ \ \ (1)$$
Podobnie, jako że $n+100 >n> k$, otrzymujemy
$$\frac{1}{n+100}< \varepsilon\ \ \ \ \ (2)$$
Dalej, odejmując stronami (2) od (1), dostajemy
$$\frac{1}{n}-\frac{1}{n+100}<0$$
$$\frac{n+100-n}{n(n+100)}<0$$
$$\frac{100}{n(n+100)}<0\ .$$
Mamy sprzeczność, bo licznik i mianownik ułamka są dodatnie, zatem cały ułamek jest dodatni.
W takim razie 1 nie jest granicą ciągu 1-1/n.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Funkcja rosnąca może mieć ujemną pochodną
Złożenie dwóch funkcji rosnących jest funkcją rosnącą, ale nie iloczyn!
Funkcja f(x) = (x-1)(x-2)(x-3) wcale nie jest rosnąca.
Każda liczba naturalna...
Jak można mówić o pochodnej funkcji zdefiniowanej na zbiorze liczb naturalnych?