stopień trudności:
- średni
- zadanie z (*) obowiązkowe na ocenę celującą
- grupy A i B mają ten sam stopień trudności
ocenianie:
23-24 - celujący
19-22 - bardzo dobry
15-18 - dobry
12-14 - dostateczny
8-11 - dopuszczający
0-7 - niedostateczny
czas pisania: 45 minut
typ sprawdzianu:
- sprawdzający wiadomości po zakończeniu działu tematycznego - wtedy zadania traktujemy jako otwarte, uczeń powinien przedstawić pełny tok rozumowania i obliczenia
- powtarzający wiadomości z danego działu przed testem kompetencji - wtedy można traktować sprawdzian jako test krótkiej odpowiedzi
grupa A (24 pkt)
Zad. 1. (2 pkt) Które z podanych przyporządkowań nie jest funkcją? Odpowiedź uzasadnij.
a) Każdej liczbie naturalnej przyporządkowujemy liczbę przeciwną.
b) Każdej liczbie trzycyfrowej przyporządkowujemy sumę jej cyfr.
c) Każdej liczbie dwucyfrowej przyporządkowujemy jej dzielniki.
Zad. 2. (4 pkt) Podaj dziedzinę oraz zbiór wartości funkcji przedstawionych na rysunkach.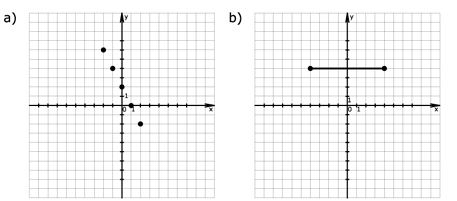
Zad. 3. (4 pkt) Funkcja f przyporządkowuje każdej liczbie ze zbioru X = {-2, -1, 0, 1.5, 3, 4} liczbę o 2 większą. Zapisz wzór tej funkcji, opisz ją za pomocą tabelki, podaj zbiór wartości, narysuj wykres.
Zad. 4. (2 pkt) Zbiór Y = {-21, -6, 3, 15} jest zbiorem wartości funkcji podanej wzorem y=-3x. Podaj dziedzinę tej funkcji.
Zad. 5. (4 pkt) Rysunek przedstawia wykres funkcji f(x). Korzystając z niego, podaj:
a) miejsca zerowe funkcji,
b) zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie,
c) przedziały, na których funkcja jest rosnąca, i przedziały, na których jest stała,
d) argumenty, dla których wartość funkcji jest największa lub najmniejsza.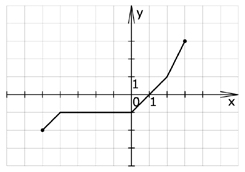
Zad. 6. (3 pkt) Funkcja g(n) każdej liczbie naturalnej przyporządkowuje resztę z dzielenia przez 7. Określ dziedzinę i zbiór wartości tej funkcji. Sporządź jej wykres dla n <20. Podaj wartość g(16).
Zad. 7. (3 pkt) Do przygotowania świątecznego ciasta na każde 0,5 kg mąki należy wziąć 4 dag drożdży.
a) Zapisz za pomocą wzoru funkcję przedstawiającą zależność masy drożdży (y) od masy mąki (x), jeśli obydwie wielkości są wyrażone w tych samych jednostkach.
b) Oblicz:
* ile należy wziąć drożdży, jeśli pieczemy ciasto z 90 dag mąki,
* ile trzeba wziąć mąki, aby upiec ciasto, dodając 7 dag drożdży.
Zad. 8.*(2 pkt) Dla jakich argumentów funkcja f przyjmuje wartości większe niż funkcja g?
grupa B (24 pkt)
Zad. 1. (2 pkt) Które z podanych przyporządkowań nie jest funkcją? Odpowiedź uzasadnij.
a) Każdej liczbie naturalnej większej od zera przyporządkowujemy liczbę odwrotną.
b) Każdej liczbie dwucyfrowej przyporządkowujemy jej wielokrotności mniejsze od 100.
c) Każdej liczbie trzycyfrowej przyporządkowujemy jej cyfrę jedności.
Zad. 2. (4 pkt) Podaj dziedzinę oraz zbiór wartości funkcji przedstawionych na rysunkach.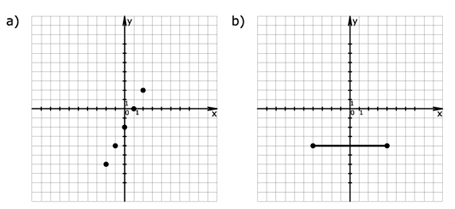
Zad. 3. (4 pkt) Funkcja f przyporządkowuje każdej liczbie ze zbioru X = {–3,–2,–0.5, 0, 2, 3} liczbę o 2 mniejszą. Zapisz wzór tej funkcji, opisz ją za pomocą tabelki, podaj zbiór wartości, narysuj wykres.
Zad. 4. (2 pkt) Zbiór Y = {-5,-4,-3, 2} jest zbiorem wartości funkcji podanej wzorem y=-2x. Podaj dziedzinę tej funkcji.
Zad. 5. (4 pkt) Rysunek przedstawia wykres funkcji f(x). Korzystając z niego, podaj:
a) miejsce przecięcia osi y,
b) zbiór argumentów, dla których funkcja przyjmuje wartości ujemne,
c) przedziały, na których funkcja jest malejąca, i przedziały, na których jest stała,
d) argumenty, dla których wartość funkcji jest największa lub najmniejsza.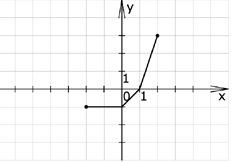
Zad. 6. (3 pkt) Funkcja f(n) każdej liczbie naturalnej przyporządkowuje resztę z dzielenia przez 6. Określ dziedzinę i zbiór wartości tej funkcji. Sporządź jej wykres dla n <19. Podaj wartość f(15).
Zad. 7. (3 pkt) Prędkość rozchodzenia się głosu w powietrzu w temperaturze 20°C wynosi 340 m/s. Za pomocą pomiarów stwierdzono, że gdy temperatura wzrasta o 1°C, prędkość głosu wzrasta o 0,6 m/s.
a) Podaj wzór funkcji wyrażającej zależność prędkości głosu (y) od temperatury powietrza (x).
b) Oblicz:
* jaka jest prędkość rozchodzenia się głosu w powietrzu w temperaturze 30°C
* jaka jest temperatura powietrza, jeśli prędkość rozchodzenia się głosu wynosi 349 m/s.
Zad. 8.* (2 pkt) Dla jakich argumentów funkcja g przyjmuje wartości mniejsze niż funkcja f?
odpowiedzi
grupa A
1. c
2. a) X = {-2, -1, 0, 1, 2}, Y = {-2, 0, 2, 3, 5} b) X =<-4, 4>, Y = {4}
3. y = x+2,zbiór wartości = {0, 1, 2, 3.5, 5, 6}
4. X = {-5, -1, 2, 7}
5. a) x=1 b) x>1 c) rosnąca na <-5, -4> oraz <0, 3>; stała na <-4, 0> d) najmniejsza wartość: -1; największa wartość:3
6. X = N, Y = {0, 1, 2, 3, 4, 5, 6}, g(16)=2
7. a) y = 0,08x; b) 7,2 dag; 0,875 dag
8. x > -1
grupa B
1. b
2. a) X = {-2, -1, 0, 1, 2}, Y = {-2,-1, 0, 1, 2} b) X =<-4, 4>, Y = {-4}
3. y = x-2, zbiór wartości = {-5, -4, -2.5, -2, 0, 1}
4. X = {-5,-1, 2, 7}
5. a) x =1 b) x<1 c) rosnąca na <0, 2>; stała na <-2, 0> d) najmniejsza wartość: -2; największa wartość:3
6. X = N, Y = {0, 1, 2, 3, 4, 5}, f(15)=3
7. a) y = 340+0,6x b) 346 m/s; 350C
8. x < -1
kryteria oceniania
1. 1 pkt za odp., 1 pkt za uzasadnienie
2. a) - b) 1 pkt za dziedzinę, 1 pkt za zbiór wartości
3. po 1 pkt za wzór, tabelkę, zbiór wartości, wykres
4. 1 pkt za przekształcenie wzoru, 1 pkt za odpowiedź
5. po 1 punkcie za a) - d)
6. 1 pkt za dziedzinę i zbiór wartości, 1 pkt za wykres, 1 pkt za wartość dla podanego argumentu
7. a) 1 pkt za wzór b) po 1 punkcie za każdy wynik
8. 1 pkt za odczytanie punktu przecięcia, 1 pkt za odpowiedź
