Graniastosłupy

autor: Katarzyna Kulawiak
studentka matematyki UWr

W poniższym teście w każdym z zadań prawdziwe mogą być: zero, jedna, dwie i więcej odpowiedzi. Zaznacz je, klikając w odpowiednie klawisze. Ponowne kliknięcie cofa zaznaczenie. Po jednym punkcie otrzymasz tylko za te zadania, w których wybierzesz wszystkie poprawne odpowiedzi.

1) Każda krawędź dolnej ściany sześcianu ma:

1a) więcej niż dwie krawędzie równoległe

1b) cztery krawędzie prostopadłe

1c) dwie krawędzie równoległe na górnej ścianie

1d) cztery krawędzie skośne

2) Każdy sześcian ma:

2a) jednakowe odległości między dowolnymi wierzchołkami

2b) sześć przekątnych

2c) więcej krawędzi niż wierzchołków i ścian razem

2d) sześć podstaw

3) Graniastosłup prawidłowy sześciokątny ma:

3a) płaszczyznę symetrii

3b) oś symetrii

3c) środek symetrii

3d) środek symetrii podstawy

4) Graniastosłup prawidłowy sześciokątny ma:

4a) 18 krawędzi, 12 wierzchołków, 6 ścian

4b) ścian i wierzchołków o 2 więcej niż krawędzi

4c) przekątnych ścian bocznych tyle co przekątnych

4d) 18 przekątnych podstaw

5) Na którym rysunku zielonym kolorem zaznaczono proste skośne, a czerwonym równoległe?

5a) I

5b) II

5c) III

5d) IV

6) Po złożeniu tej siatki naprzeciw znajdą się ściany z literami:

6a) X, Y

6b) R, Y

6c) V, S

6d) Z, Y

7) Graniastosłup i ostrosłup mają takie same objętości i równe wysokości. Wtedy:

7a) pola powierzchni całkowitych graniastosłupa i ostrosłupa są równe

7b) pole podstawy ostrosłupa jest trzy razy mniejsze od pola podstawy graniastosłupa

7c) podstawami graniastosłupa i ostrosłupa są te same wielokąty

7d) ściany boczne ostrosłupa mają te same wysokości, co graniastosłupa

8) Dla poniższych siatek zachodzi:

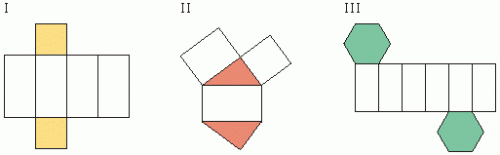
8a) tylko I i III przedstawiają siatkę graniastosłupa prostego

8b) po złożeniu II podstawy będą równoległe, a ściany boczne przystające

8c) każda ściana biała będzie prostopadła do kolorowej

8d) po złożeniu I otrzymamy graniastosłup, w którym podstawę można wybrać na dwa sposoby

9) Z której siatki nie można wykonać modelu ostrosłupa?

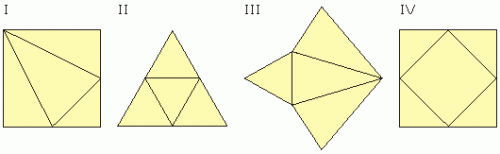
9a) I

9b) II

9c) III

9d) IV

10) Aby otrzymać sześcian z tej bryły można:

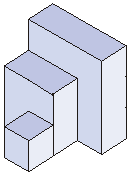
10a) dołożyć 13 kostek

10b) zabrać 13 kostek

10c) zabrać jedną kostkę i dołożyć 5

10d) zabrać dwa prostopadłościenne klocki

11) Jeśli wszystkie wymiary prostopadłościanu zwiększymy dwukrotnie, to:

11a) jego powierzchnia zwiększy się 2 razy

11b) jego objętość zwiększy się 4 razy

11c) jego szerokość zwiększy się 2 razy

11d) iloczyn długości jego wszystkich krawędzi wzrośnie 2 ¹² razy

12) W kostce sześciennej przedstawionej poniżej na każdej ściance jest jedno lub dwa oczka. Oczka są tak rozmieszczone, że w każdym położeniu kostki, na dwóch spośród trzech mających wspólny wierzchołek ściankach, znajdują się dwa oczka, a na trzeciej jedno oczko. Wtedy:

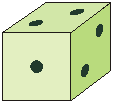
12a) na każdej z niewidocznych ścian jest tylko jedno oczko

12b) suma oczek na niewidocznych ścianach wynosi 4

12c) na równoległych ścianach jest tyle samo oczek

12d) takie rozmieszczenie jest niemożliwe

13) Po złożeniu poniższej siatki:

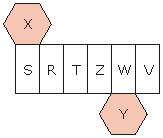
13a) ściany X i Y będą równoległe

13b) białe ściany będą prostopadłe do kolorowych

13c) ściany S i Z będą równoległe

13d) ściany T i W będą równoległe