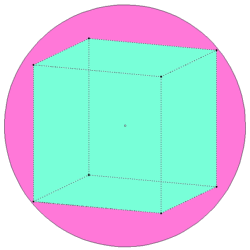
Rozważmy sześcian i opisaną na nim sferę (rys. 1).
Płaszczyzny symetrii sześcianu wyznaczają na kuli 9 kół wielkich, a okręgi ograniczające te koła tworzą na powierzchni kuli interesujący, regularny ornament (rys. 2). Jest on oczywiście ściśle powiązany z symetriami sześcianu.
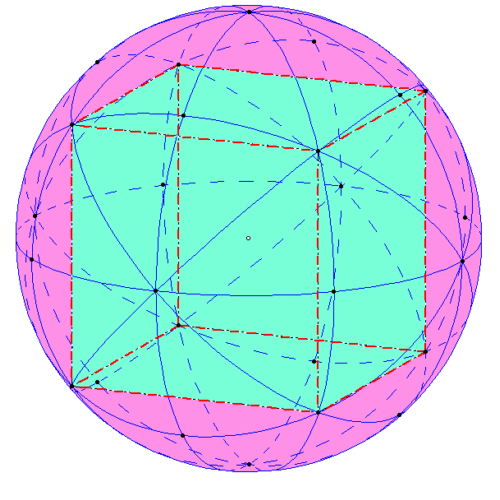
Rys. 2
Stosunkowo łatwo można skonstruować kąty środkowe odpowiadające poszczególnym łukom. Nie trzeba przy tym wykonywać w zasadzie żadnych obliczeń. Rozważmy najpierw koła wielkie przechodzące przez wierzchołki sześcianu. Takich kół jest 6 i każde z nich jest wyznaczone przez parę równoległych krawędzi, które nie należą do tej samej ściany sześcianu. Koło takie jest kołem opisanym na prostokącie, którego jeden z boków jest krawędzią sześcianu, a drugi - przekątną ściany sześcianu (rys. 3). Każdy z czterech łuków wyznaczonych przez wierzchołki prostokąta jest podzielony przez inne koła wielkie na dwie równe części (rys. 4). Każde z pozostałych trzech kół podzielone jest przez inne koła na 8 równych części (rys. 5).
Rys. 3 Rys. 4 Rys. 5
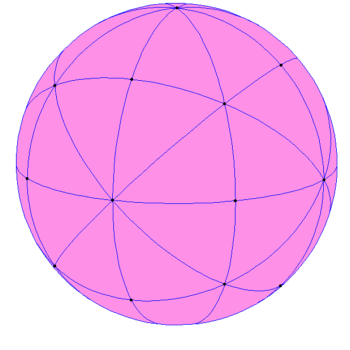
W ten sposób sfera podzielona została na 48 przystających obszarów zwanych trójkątami sferycznymi (rys. 6).
Zauważmy, że identyczną jak dla sześcianu kompozycję kół wielkich otrzymamy biorąc za wielościan bazowy ośmiościan foremny. Wynika to z faktu, że bryły te są dualne do siebie nawzajem i mają identyczne symetrie własne. Na rys. 7 zaznaczone są łuki kół wielkich odpowiadające krawędziom sześcianu, a na rys. 8 - krawędziom ośmiościanu.
Rys. 7 Rys. 8
Jest oczywiste, że analogiczną procedurę możemy zastosować do pozostałych wielościanów platońskich. Rys. 9 przedstawia odpowiednie kompozycje kół wielkich dla foremnego czworościanu (który jest dualny sam do siebie), a rys. 10 - dla foremnych i wzajemnie dualnych: dwunastościanu i dwudziestościanu.
Rys. 9 Rys. 10
Zastosowanie pewnego triku, a mianowicie zastąpienie kół pierścieniami kołowymi, pozwala na wykonanie atrakcyjnych modeli opisanych figur. Szczegóły dotyczące ich wykonania znajdują się tutaj.
Fotografie zamieszone poniżej przedstawiają modele sferyczne wykonane na bazie foremnych: 1) czworościanu, 2) sześcianu i ośmiościanu, 3) dwunastościanu i dwudziestościanu. Kliknięcie w miniaturę otwiera w nowym oknie duże zdjęcie.
Fot. 1 Fot. 2 Fot. 3
Siatka wielościanu platońskiego
Bardzo proszę o potwierdzenie, czy trójkąty tworzące powierzchnię kuli z rysunku 10 są jednakowe, tzn. czy pary trójkątów są jednakowe. Czy gdybym zrobił te trójkąty płaskie to wszystkie byłyby identyczne? Czy do stworzenia modelu tej kuli musiałbym mieć x jednakowych trójkątów lewych i x jednakowych trójkątów prawych? I to by się zamknęło? Czy mógłbym prosić o wzory na długości boków tych trójkątów w zależności od promienia kuli?
Jednakowe trójkąty
Wszystkie trójkąty są jednakowe. Do zbudowania całego modelu potrzeba 60 "lewych" i 60 "prawych". Wszystko powinno się zamknąć, ale zbudowanie modelu z płaskich trójkątów (czyli klasycznego wielościanu) jest dość trudne. Oznaczmy promień kuli przez R. Długości boków omawianych trójkątów możemy wyznaczyć z następującej zależności - są one podstawami trójkątów równoramiennych o ramionach długości R i kątach między ramionami odpowiednio równych około 20°54', 31°43, oraz 37°22'.