stopień trudności: średnio trudny
czas pisania: 45 minut
przeznaczenie: zestaw zadań może być wykorzystany na sprawdzianie, do pracy na lekcji (np. w parach) lub jako zadanie domowe
ocenianie:
25 - 30 - bardzo dobry
20 - 24 - dobry
15 - 19 - dostateczny
10 - 14 - dopuszczający
0 - 9 - niedostateczny
grupa A
Zad. 1. (3 pkt) Uzupełnij brakujące zapisy dat z historii Polski.
| rok - zapis rzymski | wydarzenie | rok - zapis arabski |
| Chrzest Polski | 966 | |
| bitwa pod Grunwaldem | 1410 | |
| MMIV | przystąpienie Polski do Unii Europejskiej |
Zad. 2. (4 pkt) Dana jest liczba A = 2004792. Nie wykonując dzielenia, oceń prawdziwość zdań (oznacz przez P zdania prawdziwe, a przez F - fałszywe). Liczba A jest podzielna przez:
a) 2 i 3,
b) 9,
c) 4, ale nie jest podzielna przez 8,
d) 5.
Zad. 3. (4 pkt) Podaj zaokrąglenie liczby 2476,99348 do:
a) tysięcy,
b) jedności,
c) części dziesiątych,
d) części setnych.
Zad. 4. (1 pkt) Wypisz liczby wymierne ze zbioru A = {–√5, [tex]\frac{3}{5}[/tex], [tex]\sqrt{1\frac{9}{16}}[/tex], –0,9, 0, [tex]\pi[/tex], √4, –1[tex]\frac{2}{3}[/tex], √2, –0,0(7), [tex]\sqrt[3]{64}[/tex]}.
Zad. 5. (2 pkt) Dane są liczby: 5, –12, [tex]\frac{4}{5}[/tex], –[tex]\frac{2}{7}[/tex], 1,2, –√6. Dla każdej z nich znajdź liczbę
a) przeciwną,
b) odwrotną.
Zad. 6. (2 pkt) Znajdź rozwinięcia dziesiętne ułamków: [tex]\frac{3}{8}[/tex], [tex]\frac{11}{40}[/tex], [tex]\frac{1}{6}[/tex], [tex]\frac{15}{22}[/tex].
Zad. 7. (1 pkt) Uszereguj rosnąco liczby: 0,2, 0,2(54), 0,(254), 0,3, 0,25(4), 0,(25).
Zad. 8. (2 pkt) Oblicz.
a) ([tex]\frac{2}{3}[/tex]·7+2[tex]\frac{1}{4}[/tex]–1[tex]\frac{5}{6}[/tex]):(–3[tex]\frac{2}{9}[/tex])
b) –(–6)+5∙[41+40:(–9–(–1))–9]
Zad. 9. (3 pkt) Na osi liczbowej zaznaczono liczby A, B i C. Oceń prawdziwość zdań (oznacz przez P zdania prawdziwe, a przez F - fałszywe). 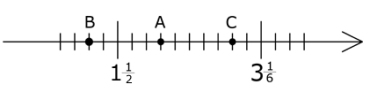
a) A = 2,2,
b) A jest średnią arytmetyczną liczb B i C,
c) odległość między liczbami B i C wynosi [tex]\frac{4}{3}[/tex].
Zad. 10. (2 pkt) Dzbanek ma pojemność 2[tex]\frac{2}{3}[/tex] litra. Sok wypełnia [tex]\frac{3}{4}[/tex] objętości dzbanka. Ile 200 ml szklanek można wypełnić tym sokiem?
Zad. 11. (4 pkt) Pan Samochodzik pojechał samochodem na wycieczkę. Po drodze przystanął na kawę i stwierdził, że ma w baku [tex]\frac{2}{5}[/tex] ilości paliwa, z którą wyjechał z domu. Zanim dojechał do celu, samochód spalił jeszcze 12 litrów, a w baku została [tex]\frac{1}{6}[/tex] paliwa, którą miał na przystanku na kawę. Z jaką ilością benzyny pan Samochodzik rozpoczął wycieczkę? Zakładając, że w drodze powrotnej samochód spali tyle samo benzyny, a jej cena to 5,75 zł, oblicz koszt tej podróży.
Zad. 12. (2 pkt) W celu wypompowania wody ze zbiornika przeciwpożarowego uruchomiono 3 pompy. Pierwsza wypompowałaby wodę ze zbiornika w ciągu 6 godzin, druga w ciągu 7godzin i 30 minut, a trzecia w ciągu 10 godzin. W jakim czasie zostanie wypompowana woda z tego zbiornika, jeśli pompy działają jednocześnie?
grupa B
Zad. 1. (3 pkt) Uzupełnij brakujące zapisy dat z historii Polski.
| rok - zapis rzymski | wydarzenie | rok - zapis arabskii |
| koronacja Bolesława Śmiałego | 1076 | |
| MDCLX | pokój w Oliwie | |
| I wizyta papieża Jana Pawła II w Polsce | 1979 |
Zad. 2. (4 pkt) Dana jest liczba A = 3103872. Nie wykonując dzielenia, oceń prawdziwość zdań (oznacz przez P zdania prawdziwe, a przez F - fałszywe). Liczba A jest podzielna przez:
a) 6,
b) 9,
c) 4, ale nie jest podzielna przez 8,
d) 5.
Zad. 3. (4 pkt) Podaj zaokrąglenie liczby 3877,98348 do:
a) tysięcy,
b) jedności,
c) części dziesiątych,
d) części tysięcznych.
Zad. 4. (1 pkt) Wypisz liczby wymierne ze zbioru A = {–√6, [tex]\frac{3}{8}[/tex], [tex]\sqrt{1\frac{17}{64}}[/tex], –0,07, 0,5[tex]\pi[/tex], √0, –2[tex]\frac{2}{7}[/tex], √3, –0,0(6), [tex]\sqrt[3]{-125}[/tex]}.
Zad. 5. (2 pkt) Dane są liczby: 4, [tex]\frac{3}{16}[/tex], –11, –[tex]\frac{3}{7}[/tex], –√5, 2,4. Dla każdej z nich znajdź liczbę
a) przeciwną,
b) odwrotną.
Zad. 6. (2 pkt) Znajdź rozwinięcia dziesiętne ułamków: [tex]\frac{5}{16}[/tex], [tex]\frac{11}{20}[/tex], [tex]\frac{1}{12}[/tex], [tex]\frac{7}{11}[/tex].
Zad. 7. (1 pkt) Uszereguj rosnąco liczby: 0,3, 0,3(52), 0,(352), 0,36, 0,35(2), 0,(35).
Zad. 8. (2 pkt) Oblicz.
a) ([tex]\frac{5}{6}[/tex]·7+1[tex]\frac{1}{4}[/tex]–1[tex]\frac{2}{3}[/tex]):(–2[tex]\frac{2}{9}[/tex])
b) 6–(–5)∙[31–30:(–7–(–1))–8]
Zad. 9. (3 pkt) Na osi liczbowej zaznaczono liczby E, F i G. Oceń prawdziwość zdań (oznacz przez P zdania prawdziwe, a przez F - fałszywe). 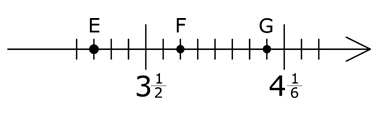
a) F= 3,6,
b) F jest średnią arytmetyczną liczb E i G,
c) odległość między liczbami E i G wynosi [tex]\frac{5}{6}[/tex].
Zad. 10. (2 pkt) Dzbanek ma pojemność 3[tex]\frac{3}{4}[/tex] litra. Sok wypełnia [tex]\frac{2}{3}[/tex] objętości dzbanka. Ile 250 ml szklanek można wypełnić tym sokiem?
Zad. 11. (4 pkt) Iza z rodzicami pojechała samochodem na wycieczkę. Po drodze przystanęli na lody i tata Izy stwierdził, że ma w baku [tex]\frac{3}{5}[/tex] ilości paliwa, z którą wyjechali z domu. Zanim dojechali do celu, samochód spalił jeszcze 11 litrów, a w baku została [tex]\frac{1}{12}[/tex] paliwa, którą mieli na przystanku na lody. Z jaką ilością benzyny rodzina rozpoczęła wycieczkę? Zakładając, że w drodze powrotnej samochód spali tyle samo benzyny, a jej cena to 5,76 zł, oblicz koszt tej podróży.
Zad. 12. (2 pkt) W celu wypompowania wody z szybu uruchomiono 3 pompy. Pierwsza wypompowałaby wodę z szybu w ciągu 9 godzin, druga w ciągu 4 godzin i 30 minut, a trzecia w ciągu 2 godzin. W jakim czasie zostanie wypompowana woda z tego szybu, jeśli pompy działają jednocześnie?
odpowiedzi
grupa A
1. Chrzest Polski - CMLXVI, bitwa pod Grunwaldem - MCDX, przystąpienie Polski do Unii Europejskiej - 2004
2. a) P, b) F, c) F, d) F
3. a) 2000, b) 2477, c) 2477 lub 2477,0, d) 2476,99
4. [tex]\frac{3}{5}[/tex], [tex]\sqrt{1\frac{9}{16}}[/tex], –0,9, 0, √4,–1[tex]\frac{2}{3}[/tex], –0,0(7), [tex]\sqrt[3]{64}[/tex]
5. a) –5, 12, –[tex]\frac{4}{5}[/tex], 1[tex]\frac{2}{7}[/tex], –1,2, √6, b) [tex]\frac{1}{5}[/tex], –[tex]\frac{1}{12}[/tex], 1[tex]\frac{2}{3}[/tex], –[tex]\frac{7}{9}[/tex], [tex]\frac{5}{6}[/tex], [tex]\frac{\sqrt{6}}{6}[/tex]
6. 0,375, 0,275, 0,1(6), 0,6(81)
7. 0,2, 0,(25), 0,(254), 0,25(4), 0,2(54), 0,3
8. a)–[tex]\frac{61}{116}[/tex], 141
9. a) F (A=2), b) P, c) F (odległość=1[tex]\frac{2}{3}[/tex])
10. 10 szklanek
11. 36 l, spalił w obie strony: 67,2 l, koszt: 386,40 zł
12. 2,5 h
grupa B
1. koronacja Bolesława Śmiałego - MLXXVI, pokój w Oliwie - 1660, I wizyta papieża Jana Pawła II w Polsce - MCMLXXIX
2. a) P, b) F, c) F, d) F
3. a) 4000, b) 3878, c) 3878 lub 3878,0, d) 3877,983
4. [tex]\frac{3}{8}[/tex], [tex]\sqrt{1\frac{17}{64}}[/tex], –0,07, √0, –2[tex]\frac{2}{7}[/tex], –0,0(6), [tex]\sqrt[3]{-125}[/tex]
5. a) –4, –[tex]\frac{3}{16}[/tex], 11, [tex]\frac{3}{7}[/tex], √5, –2,4, b) 0,25, 5[tex]\frac{1}{3}[/tex], –[tex]\frac{1}{11}[/tex], – 2[tex]\frac{1}{3}[/tex], –[tex]\frac{\sqrt{5}}{5}[/tex], [tex]\frac{5}{12}[/tex]
6. 0,3125, 0,55, 0,08(3), 0,(63)
7. 0,3, 0,3(52), 0,35(2), 0,(352), 0,(35), 0,36
8. a) –2[tex]\frac{7}{16}[/tex], b) 146
9. a) F (F=3,(6)), b) P, c) P
10. 10 szklanek
11. 20 l, spalił w obie strony: 38 l, koszt: 218,88 zł
12. 1 h 12 minut
kryteria oceniania
1. po 1 punkcie za każdą datę
2. a) - d) po 1 punkcie za poprawną odpowiedź z uzasadnieniem
3. a) - d) po 1 punkcie za odpowiedź
4. 1 pkt za wypisanie wszystkich liczb
5. a) - b) (–1) pkt za błąd
6. (–1) pkt za błąd
7. 1 pkt za poprawne uszeregowanie
8. a) - b) po 1 punkcie za wynik
9. a)- b) po 1 punkcie za odpowiedź
10. 1 pkt za obliczenie objętości soku, 1 pkt za odpowiedź
11. 1 pkt za ułożenie równania, z którego można obliczyć ilości benzyny w baku, 1 pkt za obliczenie ilości benzyny w baku i zużytej benzyny,1 pkt wyrażenie obliczające koszt, 1 pkt za poprawne obliczenia w całym zadaniu
12. 1 pkt za wyznaczenie jaką część zbiornika opróżnia każda pompa w ciągu 1 godz., 1 pkt za obliczenie czasu




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
