stopień trudności:
- średnio trudny
- zadanie z (*) obowiązkowe na ocenę celującą
- grupy A i B mają ten sam stopień trudności
ocenianie:
17 - 18 - celujący
14 - 16 - bardzo dobry
11 - 13 - dobry
9 - 10 - dostateczny
6 - 8 - dopuszczający
0 - 5 - niedostateczny
czas pisania: 45 minut
typ sprawdzianu:
- sprawdzający wiadomości po zakończeniu działu tematycznego, uczeń powinien przedstawić pełny tok rozumowania i obliczenia, starannie wykonać konstrukcje i rysunki
- może być wykorzystany jako powtórzenie wiadomości z danego działu przed testem kompetencji
Grupa A (18 pkt)
Zad. 1. (3 pkt) Skonstruuj trójkąt symetryczny do trójkąta ABC względem prostej k.
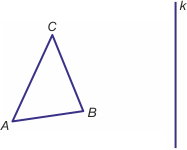
Zad. 2. (3 pkt) Dany jest odcinek AB, gdzie A=(-3, 2), B=(2, 1). Zaznacz go w prostokątnym układzie współrzędnych. Znajdź i zaznacz współrzędne odcinka symetrycznego do niego względem
a) osi x,
b) początku układu współrzędnych.
Zad. 3. (4 pkt) Na podstawie rysunku wskaż, które figury:
a) posiadają środek symetrii i nie posiadają osi symetrii
b) posiadają oś (osie) symetrii i nie posiadają środka symetrii
c) posiadają oś (osie) symetrii i środek symetrii.
Zaznacz te osie i środki symetrii.
Zad. 4. (3 pkt) Ile osi symetrii ma figura złożona z dwóch odcinków równej długości? Rozważ różne położenia tych odcinków. Odpowiedź zilustruj.
Zad. 5. (3 pkt) Oblicz obwód i pole rombu ABCD, którego środkiem symetrii jest początek układu współrzędnych. Dane są punkty A=(0, -1) i B=(4, 0).
Zad. 6*. (2 pkt) W prostokątnym układzie współrzędnych dany jest punkt A=(a, b) oraz prosta k równoległa do osi y i przechodząca przez punkt P=(5, 0). Znajdź współrzędne punktu A1 symetrycznego do A względem prostej k.
Grupa B (18 pkt)
Zad. 1. (3 pkt) Skonstruuj trójkąt symetryczny do trójkąta ABC względem punktu S.
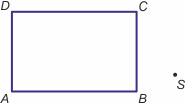
Zad. 2. (3 pkt) Dany jest odcinek AB, gdzie A=(3, 2), B=(-2, 1). Zaznacz go w prostokątnym układzie współrzędnych. Znajdź i zaznacz współrzędne odcinka symetrycznego do niego względem
a) osi y,
b) początku układu współrzędnych.
Zad. 3. (4 pkt) Na podstawie rysunku wskaż, które figury:
a) posiadają środek symetrii i nie posiadają osi symetrii
b) posiadają oś (osie) symetrii i nie posiadają środka symetrii
c) posiadają oś (osie) symetrii i środek symetrii.
Zaznacz te osie i środki symetrii.
Zad. 4. (3 pkt) Ile osi symetrii ma figura złożona z dwóch prostych? Rozważ różne położenia tych prostych. Odpowiedź zilustruj.
Zad. 5. (3 pkt) Oblicz obwód i pole rombu ABCD, którego środkiem symetrii jest początek układu współrzędnych. Dane są punkty A=(0, 3) i B=(-2, 0).
Zad. 6*. (2 pkt) W prostokątnym układzie współrzędnych dany jest punkt A=(a, b) oraz prosta k równoległa do osi x i przechodząca przez punkt Q=(0, 4). Znajdź współrzędne punktu A1 symetrycznego do A względem prostej k.
odpowiedzi
grupa A
1. rysunek
2. a) A1=(-3, -2), B1=(2, -1), b) A1=(3, -2), B1=(-2, -1)
3. a) B, b) A, c) C (8 osi), D (4 osie)
4. 1, 2 lub 4 osie
5. C=(0, 1), D=(-4, 0), pole = 8, obwód = 4√17
6. A1=(10-a, b)
grupa B
1. rysunek
2. a) A1=(-, -2), B1= (2, 1), b) A1=(-3, -2), B1=(2, -1)
3. a) B, b) A i C, c) D (2 osie)
4. nieskończenie wiele, 2 lub 4 osie
5. C=(0, -3), D=(2, 0), pole = 12, obwód = 4√13
6. A1= (a, 8-b)
kryteria oceniania
1. 2 punkty za rysunek trójkąta symetrycznego, 1 pkt za staranność
2. a) - b) po 1 punkcie za odcinek symetryczny, 1 pkt za staranność, poprawne podpisanie osi
3. gr. A a) 1 pkt b) 1 pkt c) 2 pkt za odpowiedź i rysunek, gr. B a) 1 pkt b) 2 pkt c) 1 pkt za odpowiedź i rysunek
4. po 1 punkcie za dobrze opisany każdy przypadek liczby osi
5. 1 pkt za wyznaczenie współrzędnych 2 pozostałych wierzchołków, 1 pkt za pole, 1 pkt za obwód
6. 1 pkt za rysunek z zaznaczonymi danymi, 1 pkt za podanie symetrycznego punktu
