Liczb naturalnych i parzystych jest tyle samo
Wystarczy każdą liczbę naturalną n ustawić w parze z jej podwojeniem 2n. Wtedy każda liczba naturalna stoi w parze z dokładnie jedną liczbą parzystą i żadna parzysta ani naturalna nie zostaje bez pary. To znaczy, że w tych dwóch zbiorach jest tyle samo elementów.
***
Liczb naturalnych i ułamków jest tyle samo
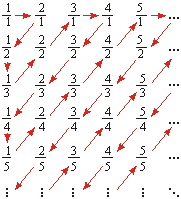
Wystarczy każdą liczbę naturalną ustawić w parze z pewnym ułamkiem, tak aby wyczerpać zbiór wszystkich ułamków. Sposób takiego ustawienia w pary (ponumerowania ułamków liczbami naturalnymi) pokazuje rysunek obok.
***
Antynomia Russela
Nie istnieje zbiór wszystkich zbiorów. Bo gdyby istniał, to musiałby też istnieć zbiór
Z = {X: X nie należy do Z}.
Ale wtedy jeśli X należy do Z, to X nie należy do Z,
a jeśli X nie należy do Z, to X należy do Z.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Nie rozumiem
Co jest paradoksalnego w równoliczności zbioru liczb parzystych ze zbiorem liczb naturalnych i zbiorem liczb wymiernych?
Coś jest
Paradoksalne jest to, że liczby parzyste są równoliczne z właściwym podzbiorem liczb naturalnych, co "dowodzi", że jest ich istotnie mniej. Przez wiele stuleci matematycy nie potrafili sobie poradzić z tego rodzaju paradoksami. To jest mało intuicyjne (bo nasze intuicje biorą się ze zbiorów skończonych - kto widział "w realu" nieskończoność?). Dziś także dla wielu ludzi jest to nie do przejścia.
Zbiór Z istnieje. To zbiór
Zbiór Z istnieje. To zbiór pusty.