Paradoks Bertranda
Prawdopodobieństwo, że wybierając losowo cięciwę okręgu trafimy na taką, której długość jest większa niż bok trójkąta równobocznego wpisanego w ten okrąg wynosi:
a) 1/2
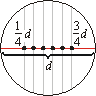
Jeśli ustalimy kierunek prowadzenia cięciw prostopadły do wybranej średnicy, to wybór dowolnej cięciwy jest równoznaczny z wyborem punktu z przedziału [0, 1], a cięciwy dłuższej niż bok trójkąta równobocznego - z wyborem punktu przedziału [1/4, 3/4].
b) 1/3
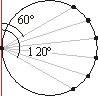
Jeśli ustalimy jeden z końców cięciwy na okręgu i poprowadzimy w tym punkcie styczną, to wybór dowolnej cięciwy jest równoznaczny z wyborem kąta z przedziału (0, 180) stopni, jaki tworzy ona ze styczną, a cięciwy dłuższej niż bok trójkąta równobocznego - z wyborem kąta z przedziału (60, 120) stopni.
c) 1/4
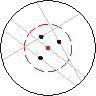
Każda cięciwa okręgu (poza średnicą) jest jednoznacznie wyznaczona przez swój środek. Wybór dowolnej cięciwy jest więc równoznaczny z wyborem punktu z wnętrza koła, a cięciwy dłuższej niż bok trójkąta równobocznego - z wyborem punktu z koła współśrodkowego o 2 razy mniejszym promieniu.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
1/3
Ten kąt musi być większy niż 60 i mniejszy niż 120 stopni, bo inaczej cieciwy będą równe, a nie większe od boków. Prosty błąd. XD
Tak właśnie jest
W treści dokładnie tak napisano (przedział jest otwarty). Ale przecież paradoks polega zupełnie na czymś innym. Chodzi o to, że zjawisko, które obiektywnie zachodzi z jakimś prawdopodobieństwem, w opisie matematycznym może mieć różne prawdopodobieństwa, w zależności od przyjętego sposobu opisu tego zjawiska. To zadziwiające. Ale pokazuje ograniczenia tzw. matematyki stosowanej. Matematyczne metody nie stosują się do życia, ale do matematycznych modeli.
Problem z nieprzeliczalnością
Wydaje mi się. że problem tkwi w tym, że operujemy prawdopodobieństwem na zbiorach nieskończonych i do tego nieprzeliczalnych. Wzory na prawdopodobieństwa mają zwykle postać stosunku liczby zdarzeń sprzyjających do liczby wszystkich możliwych zdarzeń. W podanych przykładach zdarzeń sprzyjających, niesprzyjających oraz wszystkich mamy nieskończenie wiele. A nawet można powiedzieć, że te zbiory są nieprzeliczalne (mocy continuum).
Prawdopodobieństwo geometryczne
Prawdopodobieństwo jest stosunkiem miar zbioru zdarzeń sprzyjających i wszystkich zdarzeń - zgoda. Ale miarą nie zawsze musi być moc zbioru. Może nią być pole figury, długość odcinka itp. Wtedy nieprzeliczalność zbiorów nie ma nic do rzeczy. Tak określane prawdopodobieństwo nazywa się geometrycznym.