Własności trójkątów (kl. 5)

stopień trudności:

• średniotrudny
• grupy A i B mają ten sam stopień trudności
• zadanie z (Δ) jest łamigłówką - uczeń może je rozwiązać, gdy wcześniej skończy pracę, można je uwzględnić w ocenie, gdy do kolejnego progu zabrakło 1 pkt.

ocenianie:
16-18 - celujący
14-15 - bardzo dobry
11-13 - dobry
9-10 - dostateczny
6-8 - dopuszczający
0-5 - niedostateczny

czas pisania: 45 minut

typ sprawdzianu:

• sprawdzający znajomość podstawowych własności i twierdzeń dotyczących trójkąta,
• do stosowania po zrealizowaniu cyklu lekcji o trójkątach,
• mieszany - łączy test wielokrotnego wyboru (zad. 1) z zadaniami z uzasadnieniem rachunkowym (zad. 2-7) i testem krótkiej odpowiedzi (zadanie z Δ),

Grupa A (18 pkt.)

Zad. 1. (6 pkt.) Odpowiedz "tak" lub "nie". Czy istnieje trójkąt:
a) który nie ma kąta ostrego?
b) o dwóch kątach rozwartych?
c) o bokach długości  100, 2, 100?
d) o bokach długości 2, 3, 5?
e) który ma dokładnie dwie osie symetrii?
f) którego trzy wysokości mają równe długości?

Zad. 2. (2pkt.) Obwód trójkąta równoramiennego wynosi 18 cm. Jaka jest długość podstawy tego trójkąta, jeśli jego ramię ma 7 cm?

Zad. 3. (2 pkt.) Oblicz pole trójkąta, którego wysokość ma 1 dm, a podstawa, na którą ją opuszczono, jest od niej o 4 cm krótsza.

Zad. 4. (2 pkt.) Jeden z kątów trójkąta równoramiennego ma miarę 75^o. Jakie miary mają pozostałe kąty tego trójkąta?

Zad. 5. (2 pkt.) Jeden z boków trójkąta ma długość 5 cm, a drugi jest dwa razy krótszy. Jaką długość może mieć trzeci bok tego trójkąta, jeżeli wiadomo, że jest to liczba całkowita?

Zad. 6. (2 pkt.) Długości boków trójkąta ABC wynoszą |AB|=3, |BC|=4 i |AC|=5. Odcinki |AB| i |BC| są prostopadłe. Oblicz długości wysokości tego trójkąta.

Zad. 7. (2 pkt.) Stosunek miar kątów trójkąta wynosi 1:2:3. Oblicz miary tych kątów.

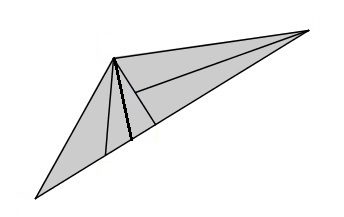
Zad. Δ (dodatkowe) Ile trójkątów jest na rysunku?

Grupa B (18 pkt.)

Zad. 1. (6 pkt.) Odpowiedz "tak" lub "nie". Czy istnieje trójkąt:
a) który ma dokładnie jeden kąt ostry?
b) o dwóch kątach prostych?
c) o bokach długości 200, 1, 200?
d) o bokach długości 1, 2, 3?
e) który ma dokładnie trzy osie symetrii?
f) którego dwie wysokości mają równe długości (a trzecia inną)?

Zad. 2. (2 pkt.) Obwód trójkąta równoramiennego wynosi 18 cm. Jaka jest długość ramienia tego trójkąta, jeśli jego podstawa ma 7 cm?

Zad. 3. (2 pkt.) Oblicz pole trójkąta, którego podstawa ma 1 dm, a opuszczona na nią wysokość  jest od niej o 5 cm krótsza.

Zad. 4. (2 pkt.) Jeden z kątów trójkąta równoramiennego ma miarę 35^o. Jakie miary mają pozostałe kąty tego trójkąta?

Zad. 5. (2 pkt.) Jeden z boków trójkąta ma długość 3 cm, a drugi jest od niego o 1,5 cm dłuższy. Jaką długość może mieć trzeci bok tego trójkąta, jeżeli wiadomo, że jest to liczba całkowita?

Zad. 6. (2 pkt.) Długości boków trójkąta ABC wynoszą |AB|=6, |BC|=8 i |AC|=10. Odcinki |AB| i |BC| są prostopadłe. Oblicz długości wysokości tego trójkąta.

Zad. 7. (2 pkt.) Stosunek miar kątów trójkąta wynosi 1:1:2. Oblicz miary tych kątów.

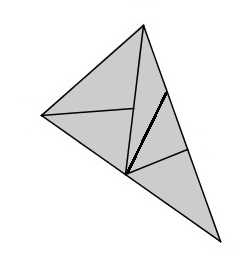
Zad. Δ. (dodatkowe) Ile trójkątów jest na rysunku?

odpowiedzi grupa A

1. a) nie, b) nie, c) tak, d) nie, e) nie, f) tak 2. 4 cm 3. 30 cm² 4. 52,5^o i 52,5^o lub 75^o i 30^o 5. 3 cm, 4, cm, 5cm, 6 cm, lub 7 cm 6. h_A=3, h_B=2,4, h_C=4, gdzie h_W-wysokość opuszczona z wierzchołka W 7. 30^o, 60^o, 90^o Δ. 10

odpowiedzi grupa B

1. a) nie, b) nie, c) tak, d) nie, e) tak, f) tak 2. 5,5 cm 3. 25 cm² 4. 72,5^o i 72,5^o lub 35^o i  110^o 5. 2 cm, 3 cm, 4, cm, 5cm, 6 cm, lub 7 cm 6. h_A=6, h_B=4,8, h_C=8, gdzie h_W-wysokość opuszczona z wierzchołka W 7. 45^o, 45^o, 90^o Δ. 10