stopień trudności: średnio trudny
czas pisania: 45 minut
przeznaczenie: zestaw może być wykorzystany na sprawdzianie, do pracy na lekcji (np. w parach) lub jako zadanie domowe
ocenianie:
25 - 30 - bardzo dobry
20 - 24 - dobry
15 - 19 - dostateczny
10 - 14 - dopuszczający
0 - 9 - niedostateczny
grupa A
W zadaniach 1-2 uzupełnij zdania.
Zad. 1. (2 pkt) 100 gramów soi zawiera m.in. 8,4 mg żelaza oraz 226 mg wapnia. W x kg soi jest … % żelaza oraz … gramów wapnia.
Zad. 2. (1 pkt) Opłata za pierwszą godzinę parkowania wynosi b zł, a za każdą następną rozpoczętą godzinę 2 zł. Za x godzin parkowania trzeba zapłacić … zł.
W zadaniach 3-4 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 3. (4 pkt) Wzór skróconego mnożenia na kwadrat sumy dwóch wielkości ma postać (a+b)2=a2+2ab+b2.
a) (... + 2)2 = 9x2 + ... + ... b) (5x + ...)2 = ... + ... + 16
A) 3x B) 12x C) 9x D) 1 E) 0 F) 6x G) 4 H) 2 I) 25x2 J) 40x K) 20x L) 25x2 M) 5x2
Zad. 4. (2 pkt) Zastosuj prawo rozdzielności mnożenia względem dodawania.
a) 4p2 + 8p = ... (p+2) b) 45p3 – 27p2 = ... (5p – ...)
A) 4 B) 8p C) 4p D) p E) 3 F) 8p2 G) 9p2 H) p2 I) 9 J) 0 K) 1
W zadaniach 5-7 wybierz poprawną odpowiedź.
Zad. 5. (1 pkt) Długości boków trójkąta równoramiennego wynoszą 2a oraz 4a+1, gdzie a>0. Obwód tego trójkąta wynosi:
A) 6a+1 B) 6a+2 C) 10a+1 D) 10a+2
Zad. 6. (1 pkt) Długość krawędzi jednego sześcianu wynosi x cm, a krawędź drugiego jest o 2 cm dłuższa. Suma pól powierzchni tych sześcianów wynosi:
A) 12x2+12x+24 cm2 B) 6x2+12x+24 cm2 C) 12x2+24x+24 cm2 D) 12x2+12x+4 cm2
Zad. 7. (1 pkt) Ania kupiła x kilogramów winogron w cenie 7,80 zł oraz mandarynki po 4,50 zł za kilogram. W sumie kupiła 8 kg owoców. Ile zapłaciła?
A) 780x+(8–x)·450 gr B) 7,80x + 8·4,50 zł C) 7,80x+4,50 zł D) (7,80+4,50)·8 zł
W zadaniach 8-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 8. (5 pkt) Zmieszano trzy gatunki cukierków: a kg po 15 zł, b kg po 20 zł i c kg po 25 zł. Cena mieszanki jest:
A) większa od 15 zł i mniejsza od 25 zł
B) równa [tex]\frac{15a+20b+25c}{a+b+c}[/tex]
C) równa [tex]\frac{15a+20b+25c}{3}[/tex]
D) równa [tex]\frac{5(3a+4b+5c)}{a+b+c}[/tex]
E) dla a=c równa [tex]\frac{15+20+25}{3}[/tex]
Zad. 9. (4 pkt) Olej z pestek winogron można kupić w dwóch rodzajach metalowych puszek w kształcie walca. Pierwsza puszka ma promień podstawy d i dwa razy dłuższą wysokość, a druga ma promień podstawy 2d i dwa razy krótszą wysokość. Olej w pierwszej puszce kosztuje 20 zł, a w drugiej 35 zł. Puszki są wykonane z takiej samej blachy.
A) I puszka ma dwa razy mniejszą objętość niż II.
B) Obie puszki mają taką samą objętość.
C) Na wyprodukowanie II puszki potrzeba dwa razy więcej blachy.
D) Bardziej opłaca się kupić olej w I puszce.
W zadaniach 10-11 zapisz podane wielkości za pomocą wyrażenia algebraicznego.
Zad. 10. (1 pkt) Różnica podwojonego kwadratu liczby a i trzeciej części sześcianu liczby b.
Zad. 11. (1 pkt) Pole figury z rysunku.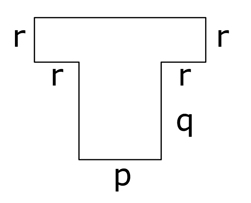
W zadaniach 12-14 odpowiedz na pytania.
Zad. 12. (1 pkt) Z metalowej płyty w kształcie prostokąta o wymiarach a cm na b cm wycięto pięć kół o promieniu r cm i trzy kwadraty o boku w cm. Jakie jest pole powierzchni pozostałej części płyty?
Zad. 13. (2 pkt) Pole powierzchni kwadratowego placu zabaw Bajka jest równe p m2. Jaką długość ma ogrodzenie również kwadratowego placu zabaw Czarodziejski Ogród, którego powierzchnia jest dwa razy większa?
Zad. 14. (4 pkt) Długości trzech krawędzi prostopadłościanu wynoszą: a–2, a+1, a+2.
a) Ile wynosi pole powierzchni całkowitej tego prostopadłościanu?
b) O ile wzrośnie pole powierzchni prostopadłościanu, jeśli każdą z krawędzi wydłużymy o 5?
c) Ile wynoszą wartości liczbowe wyrażeń z punktów a) i b) dla a=2?
grupa B
W zadaniach 1-2 uzupełnij zdania.
Zad. 1. (2 pkt) 100 g soczewicy zawiera m. in. 7,6 mg żelaza oraz 39 mg wapnia. W x kg soczewicy jest … % żelaza oraz … gramów wapnia.
Zad. 2. (1 pkt) Opłata za pierwszą godzinę parkowania wynosi a zł, a za każdą następną rozpoczętą godzinę 1,5 zł. Za y godzin parkowania trzeba zapłacić … zł.
W zadaniach 3-4 uzupełnij luki, wybierając odpowiedzi spośród podanych.
Zad. 3. (4 pkt) Wzór skróconego mnożenia na kwadrat różnicy dwóch wielkości ma postać (a–b)2=a2–2ab–b2.
a) (... – 2)2 = 9y2 – ... + ... b) (3y – ...)2 = ... – ... + 25
A) 3y B) 6y C) 12y D) 3y2 E) 9y2 F) 15y G) 30y H) 4 I) 5 J) 0 K) 1 L) 25 M) y2
Zad. 4. (2 pkt) Zastosuj prawo rozdzielności mnożenia względem dodawania.
a) 3q2 + 6q = ... (q+2) b) 54q3 – 45q2 = ... (6q – ...)
A) 3 B) 3q C) 6q D) 9q E) 9 F) 8q2 G) 9q2 H) q2 I) 5 J) 0 K) 1 L) q
W zadaniach 5-7 wybierz poprawną odpowiedź.
Zad. 5. (1 pkt) Długości boków trójkąta równoramiennego wynoszą 3a oraz 6a+2, gdzie a>0. Obwód tego trójkąta wynosi:
A) 12a+2 B) 9a+4 C) 15a+4 D) 15a+2
Zad. 6. (1 pkt) Długość krawędzi jednego sześcianu wynosi y dm, a krawędź drugiego jest o 1 dm dłuższa. Suma pól powierzchni tych sześcianów wynosi:
A) 12y2+12y+12 dm2 B) 6y2+6y +6 dm2 C) 12y2+12y+6 dm2 D) 12y2+6y+6 dm2
Zad. 7. (1 pkt) Kasia kupiła y kilogramów gruszek w cenie 5,80 zł oraz pomarańcze po 3,90 zł za kilogram. W sumie kupiła 9 kg owoców. Ile zapłaciła?
A) (5,80+3,90)·9 zł B) 3,90y+9·5,80 zł C) 5,80y+3,90 zł D) 580y+(9-y)·390 gr
W zadaniach 8-9 oceń prawdziwość odpowiedzi, oznaczając przez P - zdania prawdziwe, a przez F - fałszywe.
Zad. 8. (5 pkt) Zmieszano trzy gatunki cukierków: r kg po 12 zł, s kg po 18 zł i t kg po 24 zł. Cena mieszanki jest:
a) większa od 12 zł i mniejsza od 24 zł
b) dla r=t równa [tex]\frac{12+18+24}{3}[/tex]
c) równa [tex]\frac{12r+18s+24t}{r+s+t}[/tex]
d) równa [tex]\frac{6(2r+3s+4t)}{r+s+t}[/tex]
e) równa [tex]\frac{12r+18s+24t}{3}[/tex]
Zad. 9. (4 pkt) Oliwę z oliwek z pierwszego tłoczenia można kupić w dwóch rodzajach metalowych puszek w kształcie walca. Pierwsza puszka ma promień podstawy 3d i trzy razy krótszą wysokość, a druga puszka ma promień podstawy d i trzy razy dłuższą wysokość. Olej w pierwszej puszce kosztuje 24 zł, a w drugiej 68 zł. Puszki są wykonane z takiej samej blachy.
a) I puszka ma trzy razy większą objętość niż II.
b) Obie puszki mają taką samą objętość.
c) Na wyprodukowanie II puszki potrzeba trzy razy mniej materiału.
d) Bardziej opłaca się kupić olej w I puszce.
W zadaniach 10-11 zapisz podane wielkości za pomocą wyrażenia algebraicznego.
Zad. 10. (1 pkt) Suma potrojonego sześcianu liczby a i połowy kwadratu liczby b.
Zad. 11. (1 pkt) Pole figury z rysunku.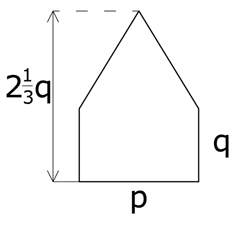
W zadaniach 12-14 odpowiedz na pytania.
Zad. 12. (1 pkt) Z metalowej płyty w kształcie prostokąta o wymiarach m cm na n cm wycięto k kół o promieniu 4 cm i trzy kwadraty o boku y cm. Jakie jest pole powierzchni pozostałej części płyty?
Zad. 13. (2 pkt) Pole powierzchni kwadratowego placu zabaw Słoneczko jest równe q m2. Jaką długość ma ogrodzenie również kwadratowego placu Promyczek, którego powierzchnia jest trzy razy większa?
Zad. 14. (4 pkt) Długości trzech krawędzi prostopadłościanu wynoszą: a–1, a+1, a+2.
a) Ile wynosi pole powierzchni całkowitej tego prostopadłościanu?
b) O ile wzrośnie pole powierzchni prostopadłościanu, jeśli każdą z krawędzi wydłużymy o 3?
c) Ile wynoszą wartości liczbowe wyrażeń z punktów a) i b) dla a=3?
odpowiedzi
grupa A
1. 0,0084%, 2,26x g, 2. b+2(x-1) zł, 3. a) A, B, G, b) G, I, J, 4. a) C, b) G, E, 5. D, 6. C, 7. A, 8. a) P, b) P, c) F, d) P, e) P, 9. a) P, b) F, c) P, d) F, 10. 2a2–[tex]\frac{1}{3}[/tex]b3, 11. rp+2r2+pq, 12. (ab–5∏r2–3w2) cm2, 13. 4[tex]\sqrt{2p}[/tex] m, 14. a) 6a2+4a–8, b) 60a+170, c) 24, 290
grupa B
1. 0,0076%, 0,39x g, 2. a+1,5(x -1)zł, 3. a) A, C, H, b) I, E, G, 4. a) B, b) G, I, 5. c), 6. c), 7. d), 8. a) P, b) P, c) P d) P, e) F, 9. a) P, b) F, c) P, d) F, 10. 3a3+[tex]\frac{1}{2}[/tex]b2, 11. 1[tex]\frac{2}{3}[/tex]pq, 12. mn–16∏k–3y2 cm2, 13. 4[tex]\sqrt{3q}[/tex] m, 14. a) 6a2+8a–2, b) 36a+78, c) 76, 186
kryteria oceniania
1-2. 1 punkt za każde uzupełnienie, 3-4. (-1) punkt za każdy błąd (do zera), 5-7. 1 punkt za odpowiedź, 8-9. 1 punkt za odpowiedź, 10-11. 1 punkt za odpowiedź, 12. 1 punkt za odpowiedź, 13. 1 pkt za długość boku, 1 pkt za odpowiedź z jednostką, 14. a)-b) 1 punkt za odpowiedź, c) po 1 punkcie za każdy wynik liczbowy
