| więcej informacji o tekście: |
Są różne zakręty: mniej lub bardziej ostre. Mogą mieć różne szerokości i kształty. Tu zajmiemy się najprostszymi, utworzonymi przez krzyżujące się dwie pary prostych równoległych, podobne do ostrego zakrętu rzeki lub raczej kanału. Przyjmiemy, że szerokość rzeki (tzn. odstęp między prostymi równoległymi) jest równa s = 20 m.
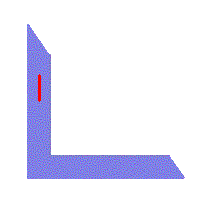
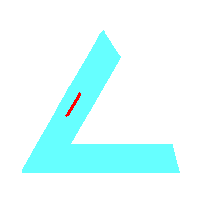

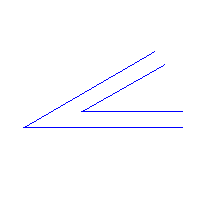
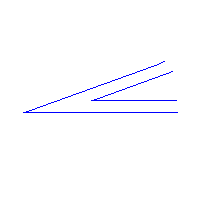
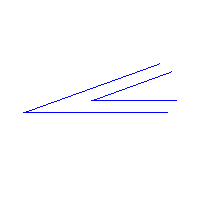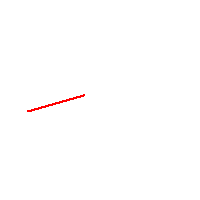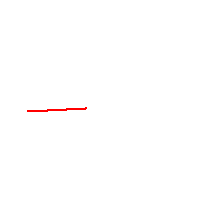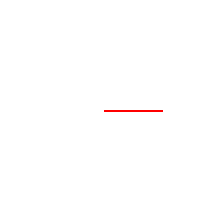
Pierwszy zakręt ma 90o, drugi jest większy, ma 120o, a trzeci - 60o. Spławiając żerdzie (pnie drzew, zaznaczone na czerwono), musimy je obrócić o takie właśnie kąty ( ).
PROBLEM Zbadamy, jakie maksymalnie długie żerdzie można spławiać tymi kanałami.
Od razu widać, że żerdzie o długości s mieszczą się bez problemu w tych zakrętach.
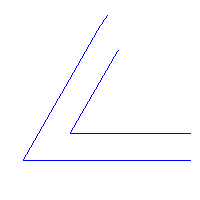
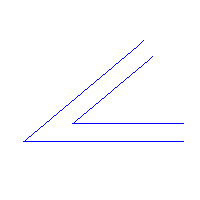
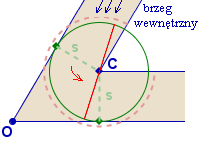 Widać też, że żerdź o długości 2s można obracać
wokół wewnętrznego cypla zakrętu (punkt C),
więc można ją spławiać wg algorytmu:
Widać też, że żerdź o długości 2s można obracać
wokół wewnętrznego cypla zakrętu (punkt C),
więc można ją spławiać wg algorytmu:
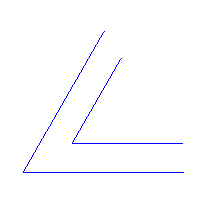
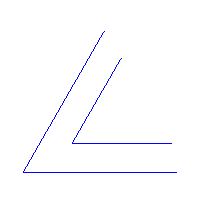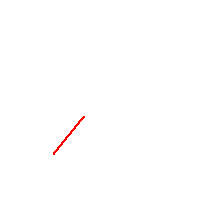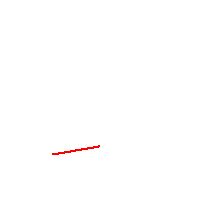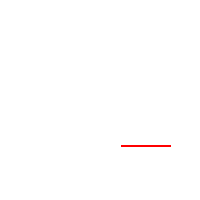
- dopłynąć do zakrętu wzdłuż wewnętrznego brzegu,
- zahamować, gdy środek osiągnie cypel C,
- obrócić wokół C o kąt równy kątowi zakrętu,
- kontynuować spławianie wzdłuż wewnętrznego brzegu.
Zaznaczony przerywaną linią okrąg pokazuje, że dłuższych żerdzi nie można spławiać... tą metodą.
Ale może można spławiać DŁUŻSZE żerdzie jakąś INNĄ metodą?

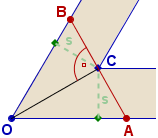 Powyższe przykłady sugerują, że newralgiczny moment, to moment, w którym
żerdź wykonała połowę obrotu. Wtedy (po ewentualnym dosunięciu jej do punktu C)
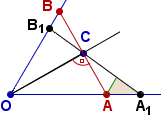
zobaczymy, że nie może być dłuższa niż odcinek AB zaznaczony na rysunku obok.
Powyższe przykłady sugerują, że newralgiczny moment, to moment, w którym
żerdź wykonała połowę obrotu. Wtedy (po ewentualnym dosunięciu jej do punktu C)
zobaczymy, że nie może być dłuższa niż odcinek AB zaznaczony na rysunku obok.
Odcinek AB jest on prostopadły do OC, C jest jego środkiem.
Gdy rzeka zakręca pod kątem prostym, AB tworzy z brzegami kąty równe 45o,
skąd można łatwo obliczyć jego długość: AB = 2 .
Gdy rzeka zakręca pod kątem 120o, AB tworzy z brzegami kąty równe
skąd można łatwo obliczyć długość: AB = 2 .
Gdy rzeka zakręca pod kątem 60o, AB tworzy z brzegami kąty równe
skąd można łatwo obliczyć długość: AB =
Ogólnie, gdy rzeka zakręca pod kątem
![]() , AB tworzy z brzegami kąty równe
skąd można wyznaczyć długość: AB =
, AB tworzy z brzegami kąty równe
skąd można wyznaczyć długość: AB =
Ciekawsze od powyższych obliczeń jest rozstrzygnięcie, czy
żerdź o długości AB można spławić przez zakręt?
Czy w innym momencie (t.j. gdy kąt pomiędzy żerdzią a OC nie jest prosty)
jest wystarczająco dużo miejsca na taką żerdź?
Poniższe twierdzenie daje na to pytanie odpowiedź twierdzącą.
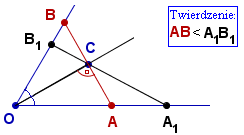 TWIERDZENIE 1.
TWIERDZENIE 1.
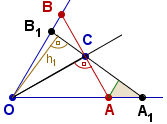
Niech punkt C leży na dwusiecznej pewnego kąta (wypukłego).
Wśród odcinków łączących ramiona tego kąta przechodzących przez
punkt C najkrótszym jest odcinek prostopadły do dwusiecznej tego kąta.
Zamiast jednego dowodu, przedstawiamy aż trzy.
Może Czytelnicy znajdą
jeszcze prostsze. Prosimy do nas napisać.
Choć nie opisaliśmy dokładnie sposobu spławiania, to wydaje się, że znaleźliśmy odpowiedź na postawiony problem.
o długościach nie większych od AB = 2s / sin(
Na koniec możecie przeczytać poniżej, co nam opowiedział praktyk. Zapytaliśmy znajomego flisaka, jak się spławia żerdzie na zakrętach.


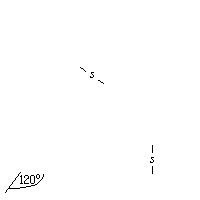



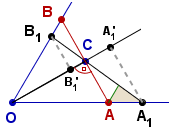 Oznaczmy przez A1' i B1'
rzuty prostokątne punktów A1 i B1 na dwusieczną OC
.
Oczywiście
A1A1' < A1C
i
B1B1' < B1C.
Oznaczmy przez A1' i B1'
rzuty prostokątne punktów A1 i B1 na dwusieczną OC
.
Oczywiście
A1A1' < A1C
i
B1B1' < B1C.
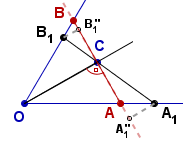 Oznaczmy przez A1'' i B1''
rzuty prostokątne punktów A1 i B1 na prostą AB
.
Oczywiście
CA1'' < CA1
i
CB1'' < CB1.
Oznaczmy przez A1'' i B1''
rzuty prostokątne punktów A1 i B1 na prostą AB
.
Oczywiście
CA1'' < CA1
i
CB1'' < CB1.






 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Opowieść doświadczonego flisaka
Drobna sprawa dotycząca zaokrąglania:
arctg2 = 63,435, zatem otrzymamy 126,87, czyli z dokładnością do jednego miejsca po przecinku 126,9.