| więcej informacji o tekście: |
|
Uwaga: nazwa 'pierwiastkowce' nie występuje w matematyce. |
Popatrz na poniższą kolekcję pierwiastkowców:
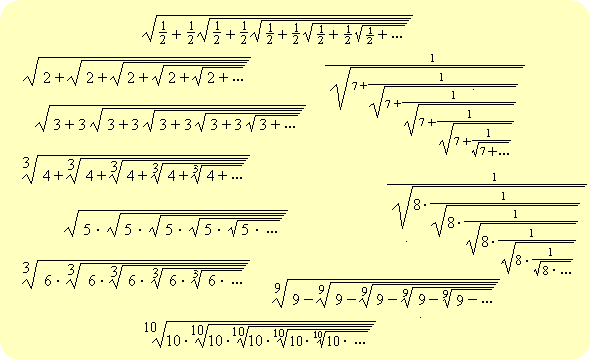
Co to właściwie jest?
Trochę przypominają one zapisy rozwinięć okresowych 0,123123123123123123....
Zatem może to są liczby?
Niektóre z tych pierwiastkowców można znaleźć w zbiorach zadań, na przykład ostatni
Czym wobec tego są pierwiastkowce?
Można uważać je za skrótowy zapis pewnych ciągów.
Na przykład pierwiastkowiec
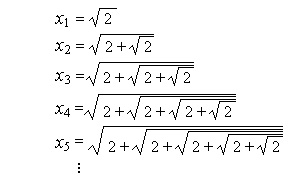
Gdy obliczamy kolejne wyrazy tego ciągu, trzeba żmudnie liczyć 'od prawej'. Na kalkulatorze, aby obliczyć piąty wyraz ciągu naciskamy sekwencję klawiszy:
Gdyby mieć taki jeden klawisz f, który do zastanej na wyświetlaczu liczby dodaje 2 i potem oblicza pierwiastek (można go zdefiniować na kalkulatorach z klawiszem ANS), to mielibyśmy:
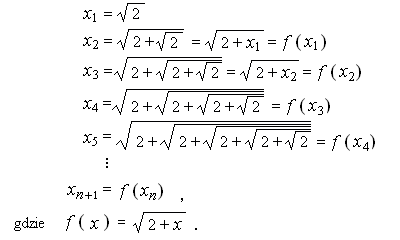
Ciekawe, że zaczynając od innych wartości początkowych, np. x0 = 2011/2012, dostajemy inny ciąg, ale zbieżny do tej samej liczby.
Za pomocą arkusza kalkulacyjnego można testować wiele takich ciągów. Sprawdź:
| f |
|
|
|
| x0 | |||
| x1 | 1,4142135623730951 | 7 | 1,731907324918789 |
| x2 | 1,8477590650225735 | 3 | 1,9318145161787112 |
| x3 | 1,9615705608064609 | 2,23606797749979 | 1,9828803585135215 |
| x4 | 1,9903694533443939 | 2,0581710272714924 | 1,9957155003941622 |
| x5 | 1,997590912410345 | 2,0144902648738445 | 1,998928588117685 |
| x6 | 1,9993976373924087 | 2,0036192914009 | 1,9997321290907153 |
| x7 | 1,999849403678289 | 2,0009046182666728 | 1,9999330311514723 |
| x8 | 1,9999623505652022 | 2,000226141781642 | 1,999983257717792 |
| x9 | 1,9999905876191524 | 2,000056534646369 | 1,9999958144250682 |
| x10 | 1,9999976469034038 | 2,0000141336116526 | 1,9999989536059932 |
| x11 | 1,9999994117257645 | 2,000003533399792 | 1,9999997384014814 |
| x12 | 1,9999998529314358 | 2,000000883349753 | 1,9999999346003692 |
| x13 | 1,9999999632328587 | 2,000000220837426 | 1,9999999836500926 |
| x14 | 1,9999999908082147 | 2,0000000552093558 | 1,999999995912523 |
| x15 | 1,9999999977020537 | 2,000000013802339 | 1,999999998978131 |
| x16 | 1,9999999994255133 | 2,0000000034505847 | 1,9999999997445326 |
| x17 | 1,9999999998563782 | 2,000000000862646 | 1,999999999936133 |
| x18 | 1,9999999999640945 | 2,0000000002156613 | 1,9999999999840332 |
| x19 | 1,9999999999910236 | 2,000000000053915 | 1,9999999999960083 |
| x20 | 1,9999999999977558 | 2,0000000000134786 | 1,9999999999990021 |
| x21 | 1,9999999999994391 | 2,0000000000033697 | 1,9999999999997504 |
| x22 | 1,9999999999998594 | 2,0000000000008424 | 1,9999999999999376 |
| x23 | 1,9999999999999647 | 2,0000000000002105 | 1,9999999999999842 |
| x24 | 1,9999999999999911 | 2,0000000000000524 | 1,9999999999999962 |
| x25 | 1,9999999999999978 | 2,000000000000013 | 1,9999999999999991 |
| a26 | 1,9999999999999993 | 2,000000000000003 | 1,9999999999999998 |
| x27 | 1,9999999999999998 | 2,000000000000001 | 2 |
| x28 | 2 | 2 | 2 |
| x29 | 2 | 2 | 2 |
| x30 | 2 | 2 | 2 |
Dla pierwszego pierwiastkowca
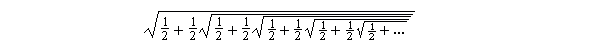
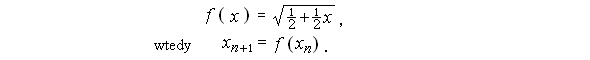
Ćwiczenie. Znajdź p takie, że
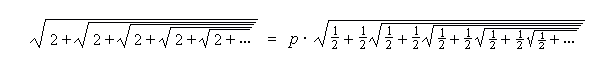
Pierwiastkowiec można też utożsamiać z liczbą będącą granicą ciągu (xn).
Obliczenia w arkuszu kalkulacyjnym przekonują, że
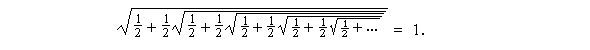
Jak obliczyć graniczną liczbę dla innych przykładów?
Ile to jest ![]() ?
?
Jeśli wiemy, że ciąg (xn) stowarzyszony z jakimś pierwiastkowcem, jest zbieżny do liczby do g,
to i xn, i xn+1 są prawie równe g, dla dużych wartości n.
Mamy
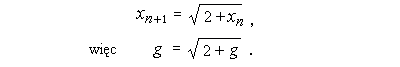
Oczywiście -1 nie może być granicą ciągu o wyrazach dodatnich, więc
Ciekawiej jest z liczbą h reprezentującą pierwiastkowiec
Pozostaje nam zadowolić się przybliżeniem z arkusza kalkulacyjnego
Jeszcze ciekawiej jest z liczbą w reprezentującą pierwiastkowiec
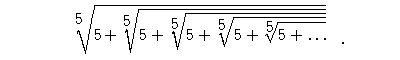
Zatem skazani jesteśmy na przybliżenia
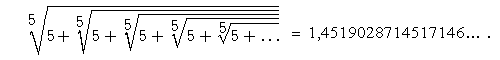
Pierwiastkowiec, a raczej związany z nim ciąg, jest (pewnym) sposobem na przybliżone rozwiązywanie niektórych równań. Tak właśnie trzeba myśleć o pierwiastkowcach.
Następny przykład jest odmienny od poprzednich. Rozważmy pierwiastkowiec
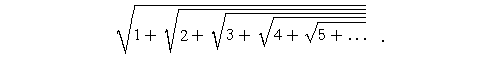
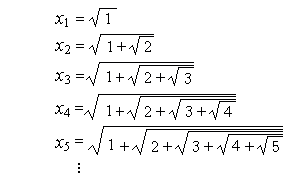
Ten ciąg oczywiście jest rosnący, ale czy jest ograniczony? Może rośnie do nieskończoności?
Potrzebny nam będzie lemat (pomocnicze twierdzenie):
Lemat 1. 2 n > n dla każdej liczby naturalnej n.
Dowód.
Pokażemy, że 4 ogranicza wszystkie wyrazy tego ciągu, pokażemy nierówność
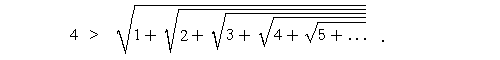
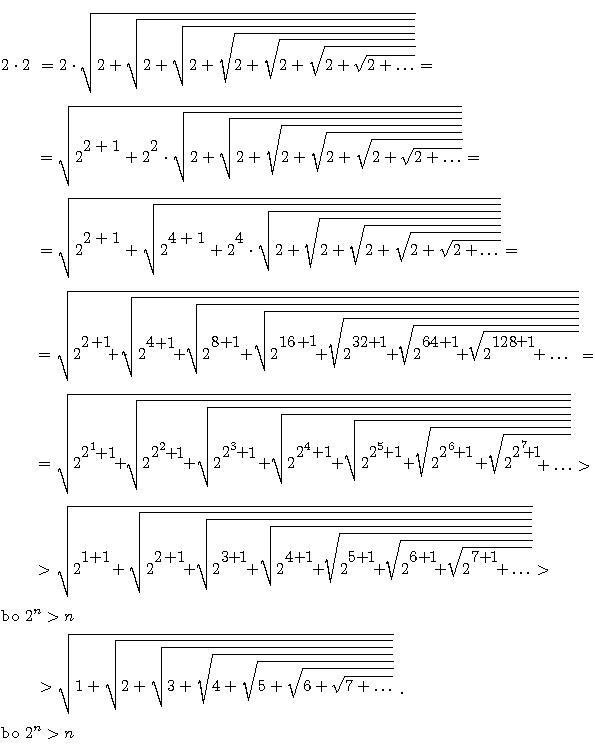
Rozważmy na koniec jeszcze jeden przykład pierwiastkowca
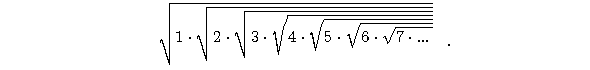
Oczywiście jest on rosnący. Czy jest ograniczony?
Sprawdź poniższe rozumowanie.
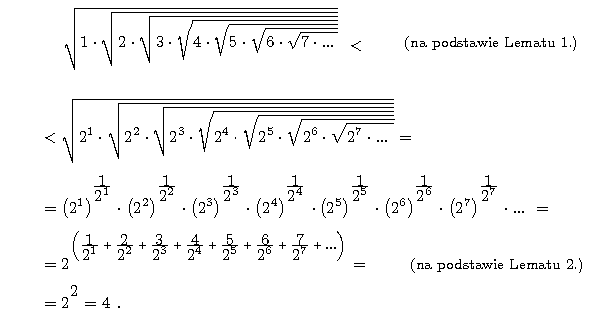
Lemat 2.
![]()
Dowód.
Oznaczmy przez z sumę
Zatem z = 1.
Pomysł dowodu lematu jest pokazany na poniższym rysunku. Prześledź to rozumowanie.
(Stając myszką nad fragmentami rysunku zobaczysz podpowiedzi.)
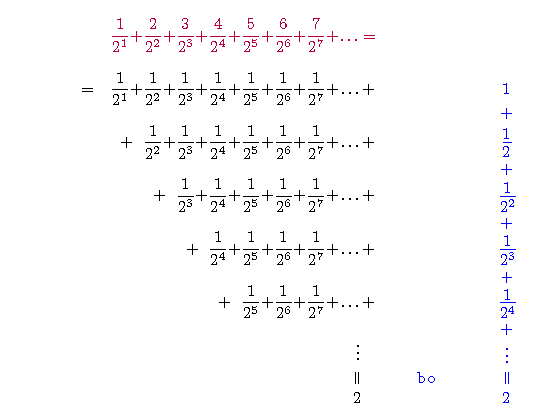














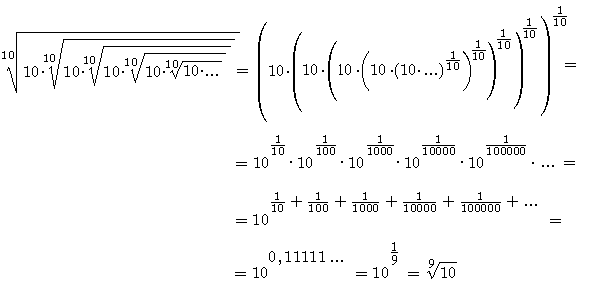
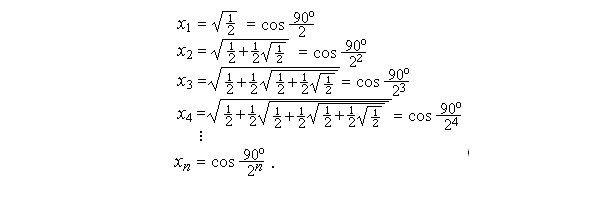
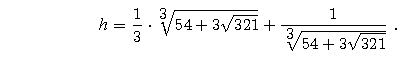



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Uwaga do samych dwójek
A mianowicie:
przekątna kwadratu o boku 1 wynosi $ d = x_1 =\sqrt{2}$,
najkrótsza przekątna ośmiokąta foremnego o boku 1 wynosi $d = x_2 =\sqrt{2+\sqrt{2}}$,
najkrótsza przekątna 16-kąta foremnego o boku 1 wynosi $d = x_3 =\sqrt{2+\sqrt{2+\sqrt{2}}}$,
najkrótsza przekątna 32-kąta foremnego o boku 1 wynosi $d = x_4 =\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}} $ , itd.
Ten ciąg wyraża więc długości najkrótszych przekątnych wielokątów foremnych o boku 1 i liczbach boków będących potęgami dwójki. Dokładniej: xn opisuje tę długość dla 2n+1-kąta foremnego.