Co właściwie oznacza "most osłów" - czyli łacińskie pons asinorum, niemieckie Eselsbrücke czy angielskie donkey bridge lub asses bridge (ass to w brytyjskim angielskim właśnie osioł, choć w amerykańskim angielskim to coś innego i to znaczenie jest dziś bardziej rozpowszechnione). Obecnie jest to termin wieloznaczny. Najkrócej rzecz ujmując, jest to "przeszkoda dla głupców". Rzecz ma jednak głębsze matematyczne konotacje sięgające czasów Euklidesa, czyli ok. 300 lat p.n.e.
To tradycyjna nazwa dowodu twierdzenia o równości kątów przy podstawie w trójkącie równoramiennym podanego przez greckiego matematyka Euklidesa jako Teza V w I księdze Elementów . To proste twierdzenie jest jednym z kluczowych w geometrii, a jego precyzyjny, dedukcyjny dowód oparty na własnościach trójkątów przystających wcale nie był taki prosty do prześledzenia. Mówiło się, że jeśli ktoś nie jest w stanie go zrozumieć i samodzielnie przeprowadzić, nie może "przekroczyć mostu" i dalej studiować geometrii.
Dziś używa się tego określenia także w szerszym kontekście - to każde zagadnienie kluczowe do zrozumienia jakiejś teorii, problem na którym testuje się niedoświadczonych adeptów danej dziedziny wiedzy i oddziela 'orły' od 'osłów'.
W językach angielskim i niemieckim termin ten oznacza także bryk (dawniej używano pochodzącego z niemieckiego słowa ezelbryk), czyli ściągę lub opracowanie lektury, dla tych, którzy nie są w stanie przeczytać oryginału. Używa się go również często na określenie chwytu mnemotechnicznego ułatwiającego zapamiętanie czegoś (czego tylko osioł nie może się nauczyć).
A jak wyglądał oryginalny "ośli most" u Euklidesa? Czy potrafisz go przekroczyć?
Elementy, księga I, teza V
Kąty przy podstawie trójkąta równoramiennego są przystające.
Dowód
założenie: AB ≡ AC
teza: ∡1 ≡ ∡2
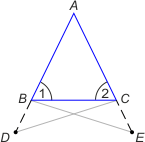
0. Przedłużamy boki AB i AC trójkąta i odmierzamy na nich cyrklem tę samą długość otrzymując punkty D i E.
A oto rozumowanie rowadzące od założenia do tezy.
1. AB ≡ AC z założenia
2. ∡A ≡ ∡A ze zwrotności relacji ≡
3. AD ≡ AE z monotoniczności dodawania (równe dodać równe daje równe)
4. ΔADC ≡ ΔAEB z cechy bkb (1-2-3)
5. DC ≡ EB z własności OCPTP (odpowiednie części przystających trójkątów przystają)
6. BC ≡ CB ze zwrotności relacji ≡
7. ΔBCD ≡ ΔCBE z cechy bbb (6-0-5)
8. ∡DBC ≡ ∡BCE z własności OCPTP
9. |∡1| = 180°–|∡DBC| z własności kątów przyległych
10. |∡2|= 180°–|∡BCE| z własności kątów przyległych
11. ∡1 ≡ ∡2 z monotoniczności odejmowania (od równych odjąć równe daje równe)
Q.E.D. (patrz tutaj - dół strony)
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
