David Wells - nauczyciel, autor podręczników i książek popularnonaukowych z matematyki, były redaktor czasopisma "Games and Puzzles"
Salonik matematyczny "Od smyka do matematyka"
ul. Racławicka 11/1B (wejście od podwórza)
53-149 Wrocław
tel. 71 361 27 41
https://matmaigry.pl/
czynne: poniedziałek–piątek, godz. 9:00–18:00

Bardzo dobra antologia łamigłówek, łakomy kąsek dla koneserów. Autor zebrał ich 568, opatrzył rozwiązaniami, starannie podał źródła pochodzenia i prześledził późniejsze warianty tej samej zagadki. Najstarsze pochodzą z egipskich papirusów i babilońskich glinianych tabliczek, wiele zaczerpnięto z XVIII-wiecznych almanachów dla kobiet i XIX-wiecznych książeczek dla młodzieży, a najnowsze - pochodzą z XX wieku i wypełniają drugą połowę książki. Pokazują, że rozwiązywanie logicznych łamigłówek od zarania dziejów było wielką pasją ludzi w każdej kulturze. Książka nie pretenduje jednak do prezentowania systematycznej historii łamigłówek. Pokazuje jedynie przykłady charakterystyczne dla danego okresu i regionu.
Staranna klasyfikacja historyczna pozwala zorientować się, że twórcami znanych do dziś łamigłówek typu "pomyśl jakąś liczbę" są starożytni Egipcjanie, Babilończycy lubili zagadki metryczne dotyczące podziału pól, Arabowie delektowali się zawiłościami islamskiego prawa spadkowego, a Chińczycy wymyślali kwadraty magiczne. Są też łamigłówki znanych autorów: Archimedesa, hinduskich matematyków - Bhakshaliego, Mahawiry i Bhaskary, średniowiecznego mnicha Alcuina i kupca z Pizy Fibonacciego, wielkich matematyków - Fermata, Newtona, Eulera oraz XIX-wiecznych mistrzów łamigłówek - Lewisa Carolla, Sama Loyda, Henry'ego Dudeneya, Eduarda Lucasa i innych. Te nazwiska są dobrze znane miłośnikom łamania głowy, ale nawet laik rozpozna wiele z prezentowanych zagadek jako te, które widział wielokrotnie w rozmaitych przedrukach. Mimo to w tak obszernym zbiorze nawet starzy wyjadacze dadzą się zaskoczyć mnóstwem zagadek i autorów, będących dla nich zupełnie nowym odkryciem (Claude de Maziriac, Henry van Etten, Wiliam Hooper, John Jackson, Jacques Ozanam i inni).
Niektóre łamigłówki są proste, inne mogą być sporym wyzwaniem nawet dla zawodowców, ale do ich rozwiązania nie jest potrzebna żadna specjalistyczna wiedza z matematyki ani logiki. Na końcu książki podano pokaźną bibliografię.
Poniżej prezentujemy kilka łamigłówek konstrukcyjnych z prac perskiego matematyka Abul Wafy (940-998).
1. Skonstruuj trójkąt równoboczny wpisany w kwadrat tak, że jeden z wierzchołków mieści się w rogu kwadratu, a pozostałe znajdują się na przeciwległych bokach.
2. Podziel trzy jednakowe kwadraty tak, aby z otrzymanych części złożyć jeden kwadrat.
3. Używając linijki i zardzewiałego cyrkla (o stałym rozwarciu), skonstruuj prostą prostopadłą do odcinka AB w punkcie A, nie przedłużając odcinka poza ten punkt.
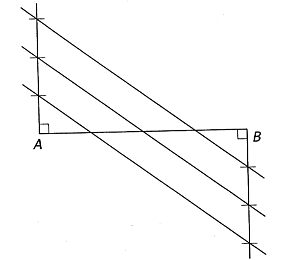
4. Używając linijki i zardzewiałego cyrkla, dokonaj podziału odcinka AB na cztery równe części.
Odpowiedzi:
Do przemyślenia. Bo przecież wiedzieć, to nie to samo, co rozumieć.
| ad 1 | ad 2 |
 |
 |
| ad 3 | ad 4 |
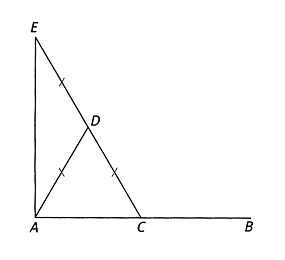 |
 |




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

zad. 1 z treści zadania
zad. 1 z treści zadania wynika że trzeba skonstruować jeden trójkąt (nie dwa ). Przeciwległe boki to nie te które mają wspólny wierzchołek (ale te równoległe).