Błąd w tablicach maturalnych

Błąd w sformułowaniu twierdzenia Talesa w tablicach maturalnych wydanych przez CKE wywołał ożywioną dyskusję wśród użytkowników Portalu, której przebieg prezentujemy w tym artykule, jako że to znacznie lepsze miejsce od poprzedniego (oryginalnie dyskusja toczyła się w dziale MATEMATYKA WOKÓŁ NAS > W literaturze > Limeryki matematyczne).

Raz pewien minister ze stolicy,
podając w maturalnej tablicy
Talesa twierdzenie,
dał mu takie brzmienie,
że śmieją się zeń nawet laicy.
                   ^{Jarosław Wróblewski, Wrocław}

A kto nie wierzy, niech sprawdzi na stronie wrocławskiej OKE (strona 8 tablic matematycznych).

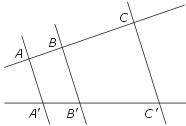
Oto stosowny cytat z tablic maturalnych CKE:
Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego)
Proste AA′, BB′, CC′ są parami równoległe wtedy i tylko wtedy, gdy zachodzi równość:

[tex]\frac{AB}{A'B'}=\frac{BC}{B'C'}[/tex].

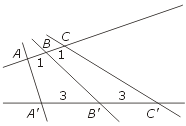Jak widać wg CKE AA′|| BB′ np. w takim wypadku jak na drugim rysunku.

Stąd już prosty wniosek, że na płaszczyźnie wszystkie proste są równoległe. Przynajmniej wg CKE. Maturzysto, strzeż się korzystania z tablic!

Błąd w tablicach polega na tym, że zachodzi tylko implikacja w jedną stronę: jeśli proste są równoległe, to podane stosunki są równe. Co w takim razie z twierdzeniem odwrotnym do twierdzenie Talesa? Przecież ono też powinno być prawdziwe, a w tym sformułowaniu ewidentnie nie zachodzi.

Na stronie CKE jest dostępna wersja poprawiona zestawu wzorów matematycznych (patrz str. 9) i errata do wydania broszurowego. Oczywiście błąd polegał na tym, że jedna z proporcji powinna dotyczyć odcinków na ramionach kąta o jednym z końców w wierzchołku kąta. Bo tylko wtedy zachodzi również twierdzenie odwrotne do twierdzenia Talesa.

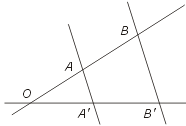Jednak CKE tak się przestraszyła poprzedniego błędu, że w erracie podała następujące sformułowanie twierdzenia: proste AA', BB', CC' są parami równoległe wtedy i tylko wtedy, gdy zachodzi równość
[tex] \frac{|OA|}{|OA'|} = \frac{|OB|}{|OB'|} = \frac{|OC|}{|OC'|}[/tex].
Ale to nie jest żadne twierdzenie Talesa. To zwykła odpowiedniość boków w trójkątach podobnych.

Błąd w tablicach na stronie CKE został poprawiony w 2006 roku. Fakt pojawienia się błędu nie jest wielkim problemem, bo błędy się zdarzają. Niepokoją natomiast dwie, dość skandaliczne, rzeczy:

1. Że po kilku latach od wykrycia błędu nie został on sprostowany na stronie wrocławskiej OKE (w roku 2009 nadal figuruje w tablicach na tej stronie).

2. Że w "poprawionej" wersji twierdzenia Talesa występują trzy proste zamiast dwóch. Obawiam się, że słabszy uczeń, na którego granicy możliwości leży zrozumienie, o co w twierdzeniu Talesa chodzi, będzie wersją z trzema prostymi mocno zdezorientowany.