Kosmiczny wzór na pole trójkąta

Każdy licealista zna co najmniej kilka wzorów na pole trójkąta, w tym taki: S = r·p, gdzie r jest promieniem okrągu wpisanego, a p - połową obwodu trójkąta. Okazuje się, że wzór ten pozostanie w mocy, gdy promień okręgu wpisanego zastąpimy promieniem okręgu opisanego, a obwód trójkąta - obwodem jego trójkąta spodkowego, czyli S = R·p_H. Kosmos?! W artykule przeprowadzimy aż 10 dowodów wyżej wspomnianego wzoru, a przy okazji poznamy kilka nowych pojęć i interesujących faktów.

Będziemy stosować następujące oznaczenia:

• S - pole trójkata ABC,
• O - środek okręgu opisanego na trójkacie ABC,
• R - promień okręgu opisanego na trójkacie ABC,
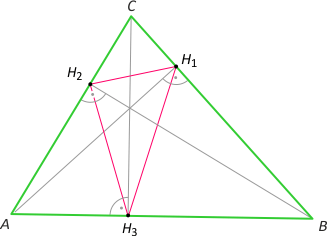
• H₁, H_2, H₃ - spodki wysokości poprowadzonych odpowiednio z wierzchołków A, B, C,
• M₁, M₂, M₃ - środki boków przeciwległych do wierzchołków odpowiednio A, B, C,
• M, N - rzuty prostokątne spodka wysokości H₃ odpowiednio na boki AC i BC,
• p_H - połowa obwodu trójkąta spodkowego H₁H₂H₃.

Przydatne definicje

1) Trójkąt spodkowy trójkąta ostrokątnego ABC to taki trójkąt wpisany w trójkąt ABC, którego wierzchołkami są spodki wysokości trójkąta ABC.

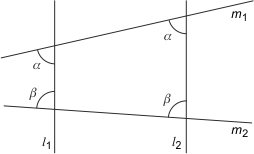
2) Antyrównoległość. Proste l₁ i l₂ są antyrównoległe (względem prostych m₁ i m₂), jeśli kąty między tymi prostymi spełniają zależność z rysunku b) poniżej.

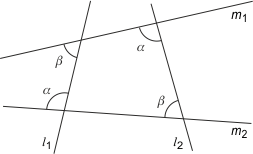a) proste równoległe	b) proste antyrównoległe

Przydatne fakty

1) Boki trójkąta spodkowego są antyrównoległe do odpowiednich boków trójkąta wyjściowego.

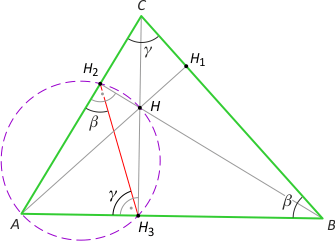
Dowód. Zauważmy, że na czworokącie AH₃HH₂ można opisać okrąg. Wówczas |∡AH₂H₃| = |∡AHH₃| (jako oparte na jednym łuku AH₃). Z kolei |∡AHH₃| = 90°–|∡H₁AB| = 90°–(90°–β) = β. Mamy zatem |∡AHH₃| = β. Analogicznie |∡AH₃H₂| = γ. Zatem bok H₂H₃ jest antyrównoległy do boku BC. Pozostałe boki - analogicznie.

2) Trójkąty AH₃H₂, BH₁H₃ i CH₂H₁ są podobne do trójkąta ABC odpowiednio w skalach k_A= cosα, k_B= cosβ i k_C= cosγ.

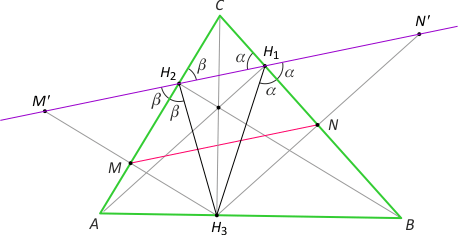
Dowód. Łatwo zauważyć, że k_A = |AH₃|:|AC| = cosα, k_B = |BH₃|:|BC| = cosβ oraz k_C = |CH₁|:|AC| = cosγ.

3) |MN| = p_H.

Dowód. Oznaczmy przez M' i N' punkty symetryczne do punktów M i N względem odpowiednich boków. Na mocy faktu 2 i własności symetrii osiowej otrzymujemy kąty jak na rysunku. Oznacza to, że punkty M', H₂, H₁ i N' są współliniowe. Łatwo zauważyć, że |M'N'| = |M'H₂|+|H₂H₁|+|H₁N'| = |H₃H₂|+|H₂H₁|+|H₁H₃| = 2p_H. Odcinek MN jest linią środkową w trójkącie M'H₃N', stąd |MN| = p_H oraz MN jest równoległy do H₂H₁.

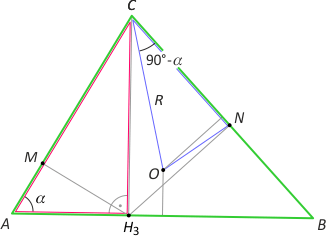
4) Łamana MON dzieli trójkąt ABC na części o równych polach.

Dowód. Zauważmy, że P_CON = ¹/₂·|CN|·R·sin(90°–α) = ¹/₂·|CN|·R·cosα oraz P_CH3A = ¹/₂·|AC|·|CH₃|·sin(90°–α) = ¹/₂·|AC|·|CH₃|·cosα. Dzieląc stronami te równości, otrzymujemy P_CON/P_CH3A = |CN|/|CH₃| · R/|AC| = ^R/_|AC|sinβ = ¹/₂. Analogicznie P_COM/P_CH3B = ¹/₂. Stąd wynika teza.

DOWODY KOSMICZNEGO WZORU

Dowód 1. Elementarny

Zauważmy, że |∡AOM₃| = γ, bo jest to połowa miary kąta środkowego AOB okręgu opisanego na trójkącie (która wynosi 2γ). Stąd |∡OAM₃| = 90°–γ. Z kolei |∡AH₃H₂| = γ, więc odcinek AO jest prostopadły do H₂H₃ i P_AH3OH2 = ¹/₂|AO|·|H₂H₃| = ¹/₂R·|H₂H₃| (pole czworokąta, w którym przekątne są prostopadłe, jest równe połowie iloczynu długości tych przekątnych). Analogicznie dla czworokątów H₃OH₁B i H₂OH₁C otrzymujemy P_H3OH1B = ¹/₂R·|H₃H₁| i P_H2OH1C = ¹/₂R·|H₂H₁|. Ostatecznie P = P_AH3OH2 + P_H3OH1B + P_H2OH1C = ¹/₂R·(|H₁H₂|+|H₂H₃|+|H₁H₃|) = R·p_H.

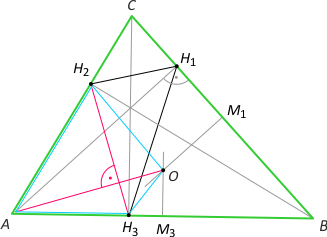
Dowód 2. Z twierdzenia sinusów

Z twierdzenia sinusów w trójkącie AH₃H₂ mamy |H₂H₃| = 2R_Asinα. Korzystając z faktu, że R_A/R = k_A = cosα, otrzymujemy |H₂H₃| = 2Rsinαcosα = Rsin2α. Analogicznie |H₁H₃| = Rsin2β oraz |H₁H₂| = Rsin2γ. Mamy zatem p_H = ¹/₂R(|H₁H₃|+|H₁H₂|+|H₂H₃|). Mnożąc obie strony tej równości przez R, otrzymujemy R·p_H = R²(sin2α+sin2β+sin2γ). Uwzględniając, że sin2α+sin2β+sin2γ = 4sinαsinβsinγ, otrzymujemy R·p_H = 2R²sinαsinβsinγ = P.

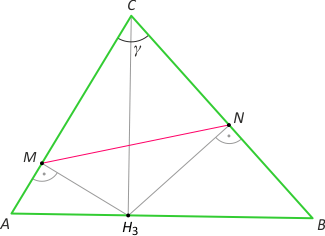
Dowód 3. Wykorzystujący interesujący odcinek MN

Zauważmy, że na czworokącie CMH₃N można opisać okrąg o średnicy CH₃. Na mocy twierdzenia sinusów w trójkącie CMN mamy |MN|/sinγ = |CH₃|, a z twierdzenia sinusów w trójkącie ABC mamy |AB| =2R·sinγ. Zatem P = ¹/₂·|AB|·|CH₃| = ¹/₂·2Rsinγ·^|MN|/_sinγ = |MN|·R. Uwzględniając fakt 3, mamy tezę.

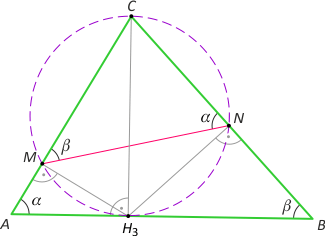
Dowód 4. Z podobieństwa trójkątów

Na czworokącie CMH₃N można opisać okrąg o średnicy CH₃. Z podobieństwa trójkątów ABC i CMN mamy |MN|:|NC| = |AB|:|AC|, skąd |MN| = ^|NC|·|AB|/_|AC|. Z kolei z twierdznia sinusów w trójkątach CMN i ABC mamy |NC|/sinβ = |CH₃| oraz sinβ = |AC|/2R. Po podstawieniu do poprzedniego wzoru otrzymujemy |MN| = (|CH₃|·^|AC|/_2R·|AB|)/AC = P/R, skąd wynika teza. 

Dowód 5. Znowu z twierdzenia sinusów

Z twierdzenia sinusów w trójkącie CMN mamy ^|MN|/_|CM| = ^sinγ/_sinα, skąd |MN| = ^sinγ/_sinα·|CM|. Dalej w trójkącie CMH₃ mamy sinα = |CM|/|CH₃|, skąd |CM| = |CH₃|sinα. Z twierdzenia sinusów w trójkącie ABC mamy sinγ = |AB|/2R. Podstawiając do poprzedniego wzoru, otrzymujemy |MN| = ^sinγ/_sinα·|CH₃|sinα = ^|AB|/_2R·|CH₃| = P/R, skąd wynika teza.

Dowód 6. Z twierdzenia kosinusów

Z twierdzenia kosinusów w trójkącie CMN mamy |MN|² = |CM|²+|CN|²–2|CM|·|CN|·cosγ. Zauważmy, że w trójkącie CMH₃ zachodzi |CM| = |CH₃|sinα, a w trójkącie CH₃N zachodzi |CN| = |CH₃|sinβ. Podstawiając do poprzedniego wzoru, otrzymujemy |MN|² = |CH₃|²sin²α + |CH₃|²sin²β – 2|CH₃|²sinαsinβcosγ = (2R·|CH₃|)²(4R²sin²α + 4R²sin²β – 2·2Rsinα·2Rsinβcosγ) = (2R·|CH₃|)²(a²+b²–2abcosγ) = (2R·|CH₃|)²·|AB|² = (P/R)², skąd |MN| = ^P/_R.

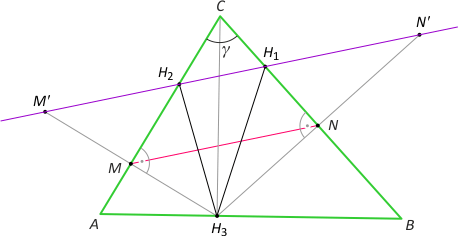
Dowód 7. Znowu z twierdzenia kosinusów

Rozważmy trójkąt CM'N'. Zachodzi |CM'|=|CN'|=|CH₃| oraz |∡M'CN'| = 2γ. Z twierdzenia kosinusów mamy |M'N'|² = |CM'|² + |CN'|² – 2|CM'|·|CN'|cos2γ = 2|CH₃|² – 2|CH₃|²cos2γ = 2|CH₃|²(1–cos2γ) = 4|CH₃|²sin²γ, skąd |M'N'| = 2|CH₃|sinγ = 2|CH₃|·^|AB|/_2R = 2^P/R. Odcinek MN jest linią środkową w trójkącie M'H₃N' i mamy |MN| = ^P/_R.

Dowód 8. I jeszcze raz z twierdzenia kosinusów

Rozważmy trójkąt MH₃N. Z twierdzenia kosinusów w tym trójkącie mamy |MN|² = |MH₃|² +|NH₃|² – 2|MH₃|·|NH₃|cos(180°–γ) = |MH₃|² + |NH₃|² – 2|MH₃|·|NH₃|cosγ. Zauważmy, że w trójkatach CMH₃ i CNH₃ mamy |MH₃| = |CH₃|cosα i |NH₃| = |CH₃|cosβ. Podstawiając do poprzedniej równości, otrzymujemy |MN|² = |CH₃|²cos²α +|CH₃|²cos²β + 2|CH₃|²cosγ = |CH₃|²(cos²α + cos²β + 2cosαcosβcosγ). Korzystając z równości (którą proponujemy udowodnić samodzielnie) 2cosαcosβcosγ = sin²α + sin²β + sin²γ – 2, mamy |MN|² = |CH₃|²sin²γ = (|CH₃|·^|AB|/_2R)² = (^P/_R)², skąd |MN| = ^P/_R.

Dowód 9. Z twierdzenia Ptolemeusza
Z twierdzenia Ptolemeusza w czworokącie CMH₃N mamy |CH₃|·|MN| = |MH₃|·|CN| + |CM|·|NH₃| = |CH₃|cosα·|CN| + |CM|·|CH₃|cosβ, skąd |MN| = |CN|cosα + |CM|cosβ = |CH₃|sinβcosα + |CH₃|sinαcosβ = |CH₃|sin(α+β) = |CH₃|sinγ = |CH₃|·^|AB|/_2R = ^P/_R.

Dowód 10. Wykorzystujący interesującą łamaną MON
Zauważmy, że odcinek MN jest równoległy do H₂H₁, a stąd jest prostopadły do CO (jak w dowodzie nr 1), zatem P_COMN = ¹/₂·R·|MN|. Wynika stąd, że |MN| = 2P_COMN/R = ^P/_R.

Dowód 11. Wykorzystujący jednokładność
Proponujemy, aby ten dowód Czytelnik przeprowadził samodzielnie.