| więcej informacji o tekście: |
Zadania optymalizacyjne, czyli polegające na znajdowanie minimum lub maksimum pewnych zmieniających się wielkości, kojarzą się większości licealistów z użyciem pochodnych. Ale wiele takich zadań można znaleźć także w dziedzinie geometrii elementarnej. Do ich rozwiązania nie są oczywiście potrzebne metody rachunku różniczkowego. Rozwiążmy kilkanaście takich zadań.
W wielu przypadkach rozwiązanie zadania optymalizacyjnego polega na wskazaniu optymalnego rozwiązania tzn. wskazaniu punktu lub odcinka optymalizującego rozważane zagadnienie (np. na podstawie intuicji), a następnie na wykazaniu, że w każdym innym przypadku rezultat będzie gorszy.
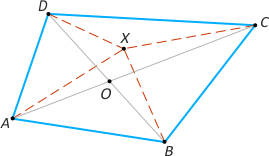
Zad. 1. W wypukłym czworokącie znajdź punkt, którego suma odległości od wierzchołków jest najmniejsza.
Rozwiązanie. Szukanym punktem jest punkt przecięcia się przekątnych czworokąta. Oznaczmy go przez O. Weźmy teraz dowolny inny punkt X. Z nierówności trójkąta mamy |AC| ≤ |AX|+|XC| oraz |BD| ≤ |XB|+|XD|. Dodając te nierówności stronami, otrzymujemy |AO|+|OC|+|BO|+|OD| = |AC|+|BD| ≤ |XA|+|XC|+|XB|+|XD|, c.n.d.
Zad. 2. Na okręgu znajdź punkty leżące a) najbliżej i b) najdalej od ustalonego punktu leżącego wewnątrz lub na zewnątrz okręgu.
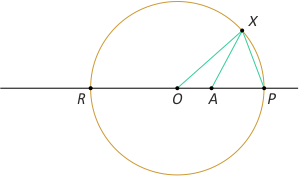
Rozwiązanie. a) Niech A będzie ustalonym punktem leżącym na zewnątrz okręgu (o promieniu r). Poprowadźmy prostą AO, która przecina okrąg w puktach P i R (niech P leży między O i A). Wówczas P leży najbliżej A, a R - najdalej. Rozważmy bowiem dowolny punkt X leżący na okręgu (różny od P i R). Mamy wówczas |AX|+|XO| > |AO| = |AP|+|PO|, ale |XO|=|PO|= r > 0, stąd |AX|>|AP|, czyli P leży najbliżej A. Z drugiej strony |AX| < |AO|+|OX| = |AO|+|OR| = |AR|, czyli R leży najdalej od A.
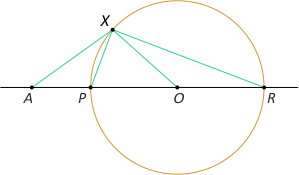
b) Niech teraz punkt A leży wewnątrz okręgu. Postępujemy jak poprzednio i otrzymamy taki sam wynik. Mamy bowiem |AO|+|AX| > |OX| = |OP| = |OA|+|AP|, czyli |AX|>|AP|. Z drugiej strony |AX| < |OA|+|OX| = |OA|+|OR| = |AR|, czyli |AX|<|AR|.
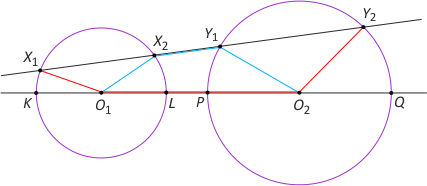
Zad. 3. Znajdź a) najkrótszy i b) najdłuższy odcinek, których końce leżą na dwóch zewnętrznie rozłącznych okręgach.
Rozwiązanie. Prowadzimy prostą przez środki okręgów O1 i O2. Niech przecina je w punktach K i L oraz P i Q, przy czym L i P niech leżą pomiędzy środkami. a) Najkrótszym odcinkiem jest LP. b) Najdłuższym KQ.
a) Rozważmy dowolną prostą, która przecina pierwszy okrąg w punktach X1 i X2, a drugi w punktach Y1 i Y2. Mamy wówczas |O1X2|+|X2Y1|+|Y1O2| > |O1O2| = |O1L|+|LP|+|PO2|, ale |O1X2|=|O1L| i |Y1O2|=|PO2|, stąd |X2Y1|>|LP|, czyli odcinek LP jest najkrótszy możliwy.
b) Mamy też |X1O1|+|O1O2|+|O2Y2| > |X1Y2|. Ale |X1O1|=|KO1| i |O2Y2|= |O2Q|, stąd |KQ|>|X1Y2|, czyli odcinek KQ jest najdłuższy możliwy.
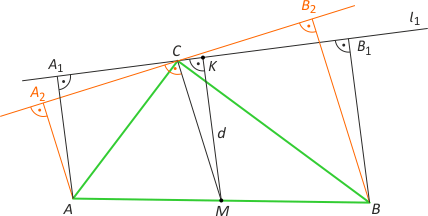
Zad. 4. Przez wierzchołek C trójkąta ABC poprowadź prostą l nie przecinającą AB, tak by suma odległości pozostałych wierzchołków od prostej l była a) największa, b) najmniejsza.
Rozwiązanie. Poprowadźmy przez wierzchołek C prostą l1. Niech A1 i B1 oznaczają odpowiednio rzuty wierzchołków A i B na tę prostą. Zauważmy, że |AA1|+|BB1| = 2|MK|, gdzie MK jest linią średnią trapezu ABB1A1. Oczywiście |MK| ≤ |MC|. Widać, że odległość MK będzie największa, gdy K pokryje się z C, co oznacza, że szukaną prostą jest prosta prostopadła do środkowej CM.
Zad. 5. Przez dany punkt wewnątrz kąta poprowadź prostą odcinającą od tego kąta trójkąt o najmniejszym polu.
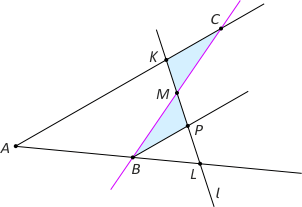
Rozwiązanie. Szukana prosta przecina ramiona kąta w punktach B i C tak, że M jest środkiem odcinka BC. Rozważmy bowiem inną prostą przechodzącą przez punkt M i przecinającą ramiona kąta w punktach K i L (różnych od B i C). Należy wykazać, że PABC < PALK. Poprowadźmy przez punkt B prostą równoległą do ramienia AC. Punkt przecięcia tej prostej z prostą KL oznaczmy przez P. Zauważmy, że trójkąty KMC i BPM są przystające na mocy cechy kbk. Mamy PABC = PABMK + PKMC < PABMK + PBPM + PBLP = PALK. Jak taką prostą narysować?
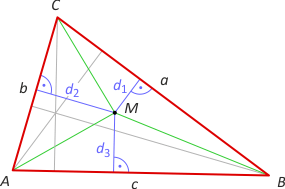
Zad. 6. Wykaż, że suma odległości dowolnego punktu z wnętrza trójkąta od jego boków jest zawarta między długościami najkrótszej i najdłuższej wysokości trójkąta.
Rozwiązanie. Niech d1, d2 i d3 oznaczają odległości punktu M odpowiednio od boków BC, AC i AB. Wówczas ad1+bd2+cd3 = 2PABC. Niech a (bok przeciwległy do A) będzie najkrótszym bokiem tego trójkąta. Wówczas ad1+ad2+ad3 ≤ 2PABC, a stąd d1+d2+d3 ≤ ha. Z kolei niech c (bok przeciwległy do C) będzie bokiem najdłuższym. Wtedy cd1+cd2+cd3 ≥ 2PABC, skąd d1+d2+d3 ≥ hc.
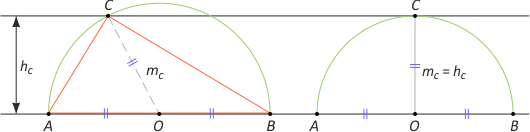
Zad. 7. Spośród trójkątów prostokątnych o stałej wysokości opuszczonej na przeciwprostokątną wskaż ten o najmniejszym polu.
Rozwiązanie. Oczywiście najmniejsze pole ma trójkąt o najkrótszej przeciwprostokątnej. Ponadto mc ≥ hc, gdzie mc to długość środkowej, a hc długość wysokości opuszczonej na przeciwprostokątną. Zatem przeciwprostokątna c = 2mc ≥ 2hc, a stąd najkrótsza przeciwprostokątna jest równa dwóm wysokościom na nią opuszczonym, co ma miejsce tylko w trójkącie równoramiennym.
Zad. 8. Wykaż, że spośród trójkątów o stałej podstawie i kącie do niej przeciwległym, trójkąt równoramienny ma najdłuższą część dwusiecznej tego kąta zawartą wewnątrz trójkąta. A jak jest w przypadku środkowej opuszczonej na podstawę?
Rozwiązanie. Niech w trójkącie ABC zachodzi |AC|=|BC|. Na trójkącie tym opiszmy okrąg i wpiszmy weń trójkąt AFB. Niech dwusieczne CW i FW przecinają AB w punktach odpowiednio D i E. Zachodzi wówczas |CD|+|DW| > |FE|+|EW| (bo średnica jest dłuższa niż cięciwa). Z drugiej strony |DW|< |EW| (bo przyprostokątna jest krótsza od przeciwprostokątnej) i stąd |CD|>|FE|.
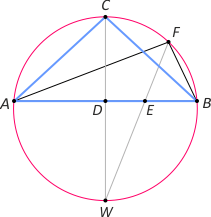
Zad. 9. W odcinek koła wpisz trójkąt o największym obwodzie L.
Rozwiązanie. Szukanym trójkątem jest trójkąt równoramienny ABC. Niech |AC|=|BC| i niech ADB będzie dowolnym trójkątem wpisanym w ten odcinek. Na prostej AC obieramy punkt C1 taki, że |CC1|=|CB|, a na prostej AD obieramy punkt D1 taki, że |DD1|=|DB|. Zauważmy, że trójkaty równoramienne CBC1 i DBD1 są podobne, bo kąty zewnetrzne ACB i ADB są przystające. Oznacza to, że kąty AC1B i AD1B maja równe miary, a tym samym punkty A, B, D1 i C1 leżą na jednym okregu, którego środkiem jest punkt C. Zatem LABC = |AB|+|AC|+|CB| = |AB|+|AC1| > |AB|+|AD1| = |AB|+|AD|+|DD1| = LABD (bo średnica AC1 jest dłuższa od cięciwy AD1).

Zad. 10. Dane są dwie styczne do okręgu poprowadzone z jednego punktu i styczna w punkcie X leżącym na krótszym łuku tego okręgu zawartym między poprzednimi punktami styczności. Wykaż, że obwód trójkąta wycietego przez te trzy styczne nie zależy od położenia punktu X.
Rozwiązanie. Niech B i C będą punktami styczności prostych AB i AC z okręgiem. Niech styczna w punkcie X przecina te styczne w punktach odpowiednio K i L. Wówczas obwód trójkąta AKL jest równy |Ak|+|KL|+|AL| = |AK|+|KX|+|XL|+|AL| = |AK|+|KB|+|LC|+|AL| = |AB|+|AC| = 2|AB|, co nie zależy od wyboru punktu X.
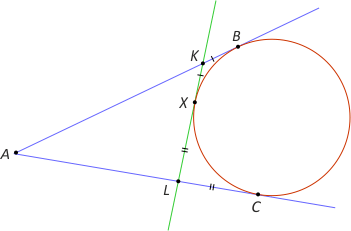
Zad. 11. Przez dany punkt wewnątrz kąta poprowadź prostą odcinającą od tego kąta trójkąt o najmniejszym obwodzie.
Rozwiązanie. Przez punkt M prowadzimy okrąg styczny do ramion kąta (jak to zrobić?). Szukaną prostą jest styczna do tego okręgu w punkcie M (która przecina ramiona kąta w punktach A i B). Rozważmy dowolną prostą l przechodząca przez M i przecinającą ramiona kąta w punktach P i Q (różnych od A i B). Istnieje styczna do okręgu równoległa do prostej PQ przecinająca ramiona kąta w punktach P1 i Q1. Oczywiste jest, że obwód trójkąta AP1Q1 jest mniejszy od obwodu trójkąta APQ. Na mocy poprzedniego zadania obwód trójkąta ABC jest najmniejszy.
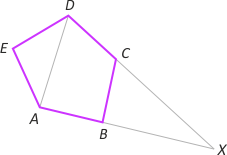
Zad. 12. Wykazać, że w wypukłym pięciokącie o wszystkich bokach równych i wszystkich kątach różnych, kąt najmniejszy i największy leżą przy jednym boku.
Rozwiązanie. Niech kąt BAE będzie największym w pięciokącie. Załóżmy nie wprost, czyli niezgodnie z tezą zadania, że np. kąt BCD jest najmniejszy. Przedłużmy boki AB i CD do przecięcia w X. Zauważamy, że |∡BAD| = |∡BAE|–|∡EAD| = |∡BAE|–|∡EDA| > |∡EDC|–|∡EDA| = |∡ADC|. Oznacza to, że w trójkącie AXD mamy |DX| > |AX|. Dalej mamy |CX| = |DX|–|DC| = |DX|–|AB| > |AX|–|AB| = |BX|. Oznacza to, że |∡CBX| = 180°–|∡ABC| > 180°–|∡DCB| = |∡BCX|, skąd |∡ABC| < |∡DCB|. Otrzymaliśmy sprzeczność z założeniem o kącie BCD. Analogicznie rozumujemy zakładając, że najmniejszym jest kąt EDC. Stąd wynika teza.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Jeszcze klasyk
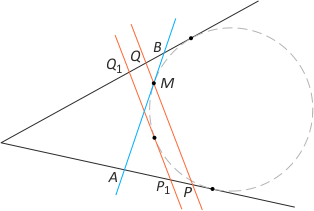
Dany jest punkt A leżący wewnątrz kąta ostrego. Znajdź trójkąt ABC o najmniejszym obwodzie, którego wierzchołki B i C leżą na ramionach tego kąta.
Rozwiązanie
Punkt A odbijamy symetrycznie w ramionach kąta, otrzymując obrazy A' i A". Niech odcinek A'A" przecina ramiona kąta w punktach B i C, które są szukanymi wierzchołkami trójkąta. Obwód trójkąta ABC jest równy długości odcinka A'A" (dlaczego?). Jeśli na ramionach kąta wybierzemy punkty B' i C' (co najmniej jeden z nich różny od B lub C), to obwód trójkąta AB'C' jest równy długości łamanej A'B'C'A", a ta jest większa niż długość odcinka A'A".
Luka
A co w przypadku, gdy odcinek A'A" nie przecina ramion kąta? Czy to jest możliwe, gdy kąt jest ostry?
Zadanie
a) Ile wynosi maksymalne pole trójkąta zawartego w kwadracie jednostkowym?
b) Ile wynosi minimalne pole trójkąta zawierającego kwadrat jednostkowy?
Rozwiązanie
a) Maksymalne pole trójkąta wynosi 1/2. Łatwo widać, że jeśli co najmniej jeden z wierzchołków P, Q, R szukanego trójkąta nie leży na brzegu kwadratu, to przesuwając go odpowiednio na brzeg, zwiększymy pole trójkąta. Jeśli natomiast wierzchołki P, Q, R trójkąta leżą na brzegu kwadratu (każdy na innym boku), to przesuwając dwa z nich do wierzchołków kwadratu, zwiększymy pole trójkata. Wówczas przesuwanie trzeciego wierzchołka wzdłuż boku kwadratu nie zmienia już pola trójkąta, a to wynosi 1/2.
b) Minimalne pole trójkata wynosi 2. Łatwo widać, że jeśli co najmniej jeden z boków szukanego trójkąta nie zawiera wierzchołka kwadratu, to odpowiednio przesuwając ten bok, zmniejszymy pole trójkąta. Jeśli natomiast trzy wierzchołki kwadratu leżą na bokach trójkąta, a czwarty nie, to odpowiednio obracajac jeden z boków trójkąta wokół wierzchołka kwadratu tak, aby leżały na tym boku dwa wierzchołki kwadratu, zmniejszymy pole trójkąta. W tej sytuacji wystarczy zastosować obserwacje z zad. 5 z artykułu: aby zminimalizować pole trójkąta, dwa wierzchołki kwadratu muszą połowić boki trójkąta, na których leżą. Oznacza to, że linia środkowa trójkąta ma długość 1, a podstawa i wysokość trójkąta mają długości 2 (dlaczego?), stąd pole trójkata wynosi 2.