Autor:
Krzysztof Omiljanowskipracownik IM UWr
Dział matematyki:
funkcje
Poziom edukacyjny:
gimnazjum
Już od pierwszego etapu kolarzy czekają wielkie trudności i mordercze podjazdy podczas górskich premii. Zobaczmy szczegółowy opis I etapu wyścigu prezentowany w formie profilu trasy, którą mają pokonać zawodnicy.
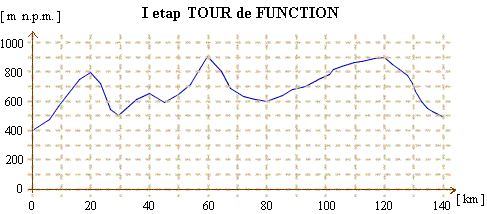
| Etap ten liczy km. | Funkcja f jest określona na przedziale | |
| Start jest na wysokości m n.p.m., a meta jest o m wyżej. |
f (0) =
,
f (140) - f (0) = |
|
| W połowie trasy, czyli na km, kolarze będą m n.p.m., a na 100 km - około m n.p.m. |
f (70) =
,
f (100) = |
|
| Osiągną 500 m już na km trasy; będą tam jeszcze na i km trasy. |
Równanie f (x) = 500
ma następujące rozwiązanie: x = lub x = lub x = . |
|
| Kolarze będą się wspinać aż na wysokość m n.p.m. i to dwukrotnie: na km i na km trasy. |
Wartością największą funkcji f jest
przyjmowane dla argumentów
x1 = oraz x2 = . |
|
|
Czekają ich 4 podjazdy:
pomiędzy a km trasy, pomiędzy i km trasy, pomiędzy i km trasy oraz pomiędzy i km trasy. Najdłuższy z nich ma aż km. |
Funkcja f jest rosnąca na przedziałach:
, , , . Najdłuższy z nich ma długość . |
|
| Podjazdy te kończą się górskimi premiami usytuowanymi na , , , kilometrze trasy. |
Funkcja przyjmuje 4 maksima lokalne w punktach:
x = ,
x = ,
x = , x = . |
Wersja: A, B, AB, C, C+odp.
Drugi etap wyścigu jest trochę mniej pofałdowany. Jednak i na nim zawodnicy będą pokonywać duże różnice wzniesień. Szczegóły można odczytać z poniższego wykresu profilu trasy.
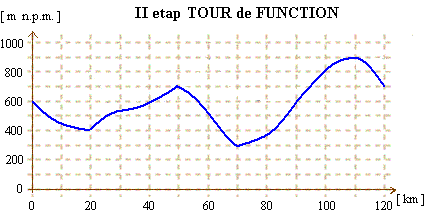
| Etap ten liczy km. | Funkcja f jest określona na przedziale |
| Start jest na wysokości m n.p.m., a meta jest o m wyżej. |
f (0) =
,
f (120) - f (0) = |
| W połowie trasy, czyli na km, kolarze będą m n.p.m., a na 100 km - m n.p.m. |
f (60) =
,
f (100) = |
| Osiągną 650 m na km trasy; będą tam jeszcze na i km trasy. |
Równanie f (x) = 650
ma następujące rozwiązanie: x = lub x = lub x = . |
| Kolarze będą się wspinać aż na wysokość m n.p.m.; osiągną ją na km trasy. | Wartością największą funkcji f jest przyjmowane dla argumentu x = . |
|
Czekają ich tylko 2 podjazdy (ale za to długie):
pomiędzy a km trasy oraz pomiędzy a km trasy. Dłuższy z nich ma aż km. |
Funkcja f jest rosnąca na przedziałach:
, . Dłuższy z nich ma długość . |
| Podjazdy te kończą się górskimi premiami usytuowanymi na , kilometrze trasy. | Funkcja przyjmuje 2 maksima lokalne w punktach: x = , x = . |
Wersja: A, B, AB, C, C+odp.
Najtrudniejszy jest trzeci etap. Trasę wytyczono w kształcie dwunastokilometrowej pętli, którą kolarze będą przemierzać 10 razy. Szczegóły jednego okrążenia można odczytać z poniższego wykresu profilu.
| Na jakiej wysokości nad poziomem morza znajduje się meta wyścigu? |
| Na jakiej wysokości znajdą się kolarze po przejechaniu 1/4 trasy? |
| Na jakiej wysokości znajdą się kolarze po przejechaniu 3/4 trasy? |
| Ile razy będą dokładnie 800 m n.p.m.? |
| Ile jest zjazdów? |
| Jaka jest długość najkrótszego ze zjazdów? |
| Jaka jest łączna długość zjazdów? |
| Jaki procent trasy stanowią zjazdy? |
| Jaką największą różnicę wzniesień pokonają kolarze na jednym podjeździe? |
| Jaka jest łączna długość podjazdów? |
| Jakie łączne przewyższenie pokonają kolarze na całej trasie? |
|
Ile kilometrów kolarze jechać będą powyżej 600 m n.p.m.?
Jaki to procent całej trasy? |
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
fajoweeeee!!!!!
fajoweeeee!!!!!
taaaak
taaaak