Instytut Matematyczny Uniwersytetu Wrocławskiego
pl. Grunwaldzki 2/4, 50-384 Wrocław
strona domowa Maratonu
15 IX 2011, godz. 8-14 eliminacje dla wrocławskich SP i GIM
16 IX 2011, godz. 8-14 eliminacje dla wrocławskich szkół ponadgimnazjalnych i szkół pozawrocławskich
17 IX 2011, godz. 8-9 eliminacje "last minute"
17 IX 2011, godz. 10-24 (lub dłużej) finały
Grupy obowiązuje rezerwacja miejsc. Można jej dokonać od 1 IX 2011 za pomocą formularza internetowego na stronie domowej konkursu.
Rozwiązywanie zadań "do upadłego" jest świetną zabawą i przygodą z matematyką dla jej fanów. Na wrocławski maraton niektórzy przyjeżdżają specjalnie z odległych miejscowości, a nawet z zagranicy. W każdej kategorii wymagana jest wiedza ze szczebla niższego (dla gimnazjalisty ze szkoły podstawowej, dla studenta z zakresu matury itd.). Zadania są ciekawe i zróżnicowane. Liczy się nie tylko znajomość matematyki, ale pomysłowość i wytrzymałość fizyczna. Co roku w Maratonie startuje ponad 2500 zawodników (w roku 2008 - 3500).
Szczegóły są na stronie domowej Maratonu.
Maratony Matematyczne organizowane są podczas Dolnośląskich Festiwali Nauki od 2001 roku (IV DFN) z przerwą w roku 2004 (VII DFN). W 2011 roku jubileuszowy X Maraton otworzył wiceprezydent Wrocławia Jarosław Obremski, a specjalne upominki dla swoich następców ufundowali zwycięzcy I edycji w poszczególnych kategoriach.
W latach 2004 i 2006 zorganizowane zostały przez wrocławskich studentów pod patronatem Magazynu Miłośników Matematyki zamiejscowe MiniMaratony Matematyczne z okazji zjazdu Polskiego Towarzystwa Matematycznego w Białymstoku i Forum Matematyków Polskich w Gdańsku.
Wrocławskie maratony znalazły już pierwszych naśladowców. Od kilku lat odbywają się podobne imprezy w I LO w Piotrkowie Trybunalskim i II LO w Jeleniej Górze, od 2008 roku ruszył maraton w Warszawie, od 2009 roku w Łodzi, a od 2010 w Szczecinku.
Zwycięzcy Wrocławskich Maratonów Matematycznych:
- 2001 - I MM
SP Witold Świątkowski (SP 91 Wrocław)
GIM Bartłomiej Andrzejewski (G 1 Opole)
LO Marcin Preisner (I LO Jelenia Góra)
PROF Piotr Kryszkiewicz (nauczyciel matematyki, ZS nr 2 Milicz) - 2002 - II MM
SP Bartłomiej Trocha (SP 91 Wrocław)
GIM Michał Molicki (G 49 Wrocław)
LO Andrzej Łątka (XIV LO Wrocław)
AMAT Waldemar Bednarz (inżynier elektronik z Wrocławia)
PROF Stanisław Klekot (student PWr) - 2003 - III MM
SP Mariusz Olszewski (SP 90 Wrocław)
GIM Andrzej Zając (G Bolków)
LO Michał Chrzanowski (IX LO Wrocław)
AMAT Waldemar Bednarz (inżynier elektronik z Wrocławia)
PROF Sebastian Gąsior (student PWr) - 2005 - IV MM
SP Michalina Sieradzka (SP 93 Wrocław)
GIM Andrzej Moskal (G 1 Wrocław)
LO Stanisław Klajn (II LO Lubin)
AMAT Ewa Piekarska (gospodyni domowa z Wrocławia, babcia Ani)
PROF Filip Sieczkowski (student PWr) - 2006 - V MM
SP Jakub Sutowicz (SP 60 Wrocław)
GIM Aleksander Małecki (G 23 Wrocław)
LO Andrzej Zając (II LO Jelenia Góra)
AMAT Robert Motyka (Bogatynia)
PROF Waldemar Bednarz (inżynier elektronik z Wrocławia) - 2007 - VI MM
SP Kamil Niziński (SP 64 Wrocław)
GIM Maciej Tyszko (G 49 Wrocław)
LO Mikołaj Hojko (III LO Wrocław)
AMAT i PROF Piotr Mazur (urzędnik ze Złotoryi) - 2008 - VII MM
SP Paweł Berezowski (SP Środa Śląska)
GIM Mateusz Gołębiewski (G 49 Wrocław)
LO Krzysztof Nowicki (LO 14 Wrocław)
AMAT Piotr Mazur (urzędnik ze Złotoryi)
PROF Piotr Pawlikowski (nauczyciel matematyki, I LO Kluczbork) - 2009 - VIII MM
SP Agnieszka Dudek (SP 3 Wrocław)
GIM Kamil Dzikowski (G 49 Wrocław)
LO Agata Gniewek (LO 14 Wrocław)
PROF/AMAT Waldemar Bednarz (inżynier elektronik z Wrocławia) - 2010 - IX MM
SP Dawid Ignasiak (SP 24 Wrocław)
GIM Michał Hadryś (GIM 49 Wrocław)
LO Mateusz Gołębiewski (LO 14 Wrocław)
AMAT Robert Motyka (doradca podatkowy z Bogatyni), Piotr Mazur (urzędnik ze Złotoryi)
PROF Waldemar Bednarz (inżynier elektronik z Wrocławia) - 2011 - X MM
SP Dawid Ignasiak (SP 24 Wrocław)
GIM Maciej Kucharski (GIM 49 Wrocław)
LO Radosław Serafin (LO 3 Wrocław)
AMAT Piotr Mazur (urzędnik ze Złotoryi)
PROF Damian Straszak (student informatyki UWr)
Eliminacje polegają na wypełnieniu karty zgłoszenia i rozwiązaniu testu kwalifikacyjnego w czasie 45 minut. W ciągu 15 minut po oddaniu testu zawodnik dowiaduje się, czy zakwalifikował się do finału (wywieszane są kartki z nazwiskami finalistów). Wyniki publikowane są też w Internecie. W eliminacjach można brać udział tylko jeden raz.
Finał rozgrywany jest w sobotę od godz. 10.00. Rundy zaczynają się o pełnych godzinach i trwają 40 minut. W każdej do rozwiązania jest inny rodzaj testu. Przed następną rundą ogłaszane są nazwiska odpadających zawodników. Mogą oni zgłosić reklamację i w razie jej uznania, przywracani są do gry. Zawody kończą się, gdy w danej kategorii w grze pozostanie jeden zawodnik. Zajmuje to zazwyczaj od 12 do 18 godzin.
Uczestnicy finału poniżej 16 roku życia jeśli zakończą grę po godzinie 20:00, muszą zostać odebrani z Instytutu Matematycznego przez dorosłego opiekuna (o zakończeniu gry mogą go powiadomić telefonicznie na koszt organizatorów). Uczestnikom zamiejscowym powyżej 16 roku życia, kończącym grę po godzinie 24:00 organizatorzy zapewniają miejsce do spania na podłodze Instytutu. Trzeba zabrać karimaty i śpiwory.
SZKOŁA PODSTAWOWA
Przy każdej odpowiedzi zaznacz, czy jest prawdziwa, czy nie.
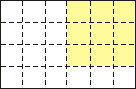1. Jaką część pola dużego prostokąta stanowi zamalowany prostokąt?
a) 3/8 b) 6/24 c) 37,5% d) 1/4
2. Czy jest to liczba całkowita?
a) b)
c)
d)
3. Która liczba daje resztę 1 przy dzieleniu przez 5?
a) 1 000 001 b) 888 c) 16·55555 d) 1234·55555+6
GIMNAZJA
Czy to możliwe, żeby...
1.
a) liczba, o której można powiedzieć w przybliżeniu "kilkadziesiąt", miała w zapisie rzymskim 8 cyfr?
b) Wacek z czwartej klasy przeżył do dziś od urodzenia 6 milionów sekund?
c) 455 było w przybliżeniu równe 0?
d) cyfra setek trzycyfrowej liczby była zerem?
e) na osi liczbowej liczba mniejsza leżała na prawo od większej?
2.
a) jakaś krawędź i jakaś ściana sześcianu nie miały punktów wspólnych?
b) 3 różne krawędzie sześcianu były równolegle?
c) 5 krawędzi sześcianu leżało na jednej płaszczyźnie?
d) 4 krawędzie sześcianu miały jeden punkt wspólny?
e) cieniem sześcianu był sześciokąt?
3.
a) prostokąt miał równoległe przekątne?
b) czworokąt miał dokładnie dwa kąty rozwarte?
c) wielokąt miał dokładnie 23 boki?
d) wielościan miał dokładnie 23 ściany?
e) ostrosłup miał większą objętość niż graniastosłup o tej samej podstawie?
PONADGIMNAZJALNE
Przy każdej odpowiedzi zaznacz, czy jest prawdziwa, czy nie.
1. Jeśli a < b, to:
a) a należy do <a, b>
b) b nie należy do (a, b)
c) (a+b)/2 należy do (a, b)
d) ab nie należy (a, b)
2. Pierwsza maszyna robi od 80 do 100 zabawek na minutę i średnio 5300 zabawek na godzinę, a druga od 100 do 120 takich samych zabawek na minutę i średnio 6400 na godzinę, to pracując razem będą wytwarzać:
a) od 190 do 210 zabawek na minutę
b) średnio 195 zabawek na minutę
c) średnio na jedną maszynę 5850 zabawek na godzinę
d) nie więcej niż 220 zabawek na minutę
3. 30% mieszkańców Nauru to osoby mające nie więcej niż 25 lat, a 80% mieszkańców ma już żonę lub męża. Wszystkie małżeństwa mieszkają wspólnie w tym kraju. Liczba osób, których współmałżonek liczy nie więcej niż 25 lat.
a) nie może przekraczać 30% ludności kraju
b) może przekroczyć 30%, ale nie może przekraczać 60% ludności kraju
c) nie może być mniejsza niż 20% ludności kraju
d) jest równa dokładnie 45% ludności kraju
W jakim mieście położonym na tej samej szerokości geograficznej co Wrocław 1 maja słońce wzeszło o 6:15? Odpowiedź znajdziesz w Lidze Zadań „Z kalkulatorem i komputerem”. 
Rozkwitają kasztany. To znak, że zaczyna się maturalna gorączka. Polecamy wzorcowe rozwiązania arkuszy archiwalnych z matematyki na stronie 
Zapraszamy do malowniczego Kluczborka na Opolszczyźnie, gdzie do 27 V w muzeum regionalnym można zwiedzać wystawę modeli wielościanów z naszej portalowej Galerii autorstwa Piotra Pawlikowskiego.
