Zad. 1. Ile cyfr może mieć iloczyn liczb stu- i dwustucyfrowej?
Zad. 2. Jak wygląda zbiór punktów płaszczyzny, których współrzędne spełniają równanie x|y|=|x|?
Zad. 3. Oblicz obwód figury, jaką tworzą punkty leżące w odległości mniejszej lub równej 1 od trójkąta o bokach 7, 8, 9.
Rozwiązania zadań czerwcowych przysłała tylko Michalina Sieradzka z G 49 Wrocław. Dwa z nich były poprawne.
W roku szkolnym 2007/08 w Lidze Zadaniowej Gimnazjów brało udział zaledwie 10 osób. Była to najmniej liczna spośród wszystkich lig na Portalu, ale mamy nadzieję, że w przyszłym roku szkolnym uczestników będzie więcej.
Najwięcej punktów (20,5 na 27 możliwych) zdobyła Michalina Sieradzka - G 49 Wrocław. Gratulujemy! Nagrody - książki, łamigłówki i sprzęt sportowy - wyślemy pocztą.
Zapraszamy wszystkich gimnazjalistów do wspólnej zabawy od października!
Zad. 1. Najmniejszy taki iloczyn to jedynka i 298 zer, największy zaś wynosi
(10100 - 1)(10200 - 1) = 10300 + 1 - (10200 + 10100).
Widać, że liczba z prawej strony równości ma 300 cyfr. Odpowiedzią jest więc 299 lub 300.
Zad. 2. Jeśli x=0, to równanie jest spelnione. Jeśli nie, to po podzieleniu obu stron przez x otrzymujemy, że |y|=1, jeśli x>0, a jeśli x jest ujemne, |y| miałby być równy (-1), co nie jest możliwe. Ostatecznie równanie spełniają pary (0, y) dla dowolnego y oraz pary (x, 1) i (x, -1) dla x>0, co przedstawia rysunek: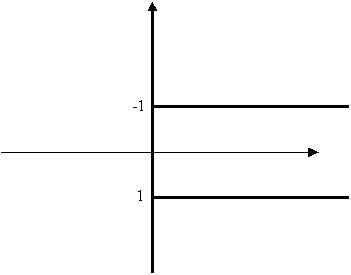
Zad. 3. Figura ta ograniczona jest odcinkami o długościach 7, 8 i 9 oraz trzema łukami okręgu o promieniu 1, składających się w sumie na cały okrąg. Jej obwód to zatem 24+2π.
Tradycja bożo-narodzeniowych jarmarków we Wrocławiu sięga XVI wieku. Jedną z ich atrakcji bywała dawniej "legnicka bomba". Co to było? 
