Zad. 1. Dana jest szachownica n x n, której wszystkie pola są białe. Jaką największą liczbę pól można pomalować na czarno tak, aby w każdym kwadracie 2 x 2 zawartym w szachownicy znalazły się co najwyżej dwa pola czarne?
Zad. 2. Wykaż, że jeśli funkcja f jest liniowa, to dla dowolnych liczb rzeczywistych a i b zachodzi równość f(a+b) + f(a–b) = 2f(a).
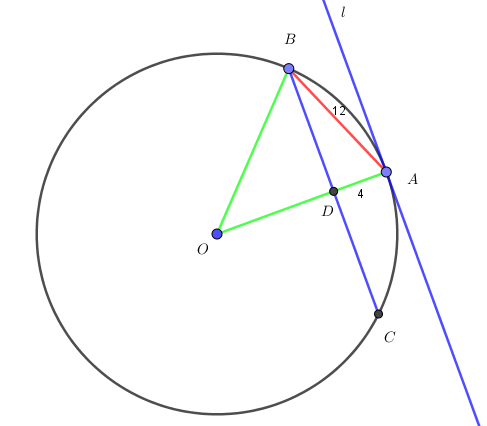
Zad. 3. Przez punkt A leżący na okręgu o środku O poprowadzono styczną l oraz cięciwę AB o długości 12. Oblicz stosunek pola trójkąta BOC do pola czworokąta OBAC, jeśli BC jest cięciwą tego okręgu równoległą do prostej l i odległą od niej o 4.
W czerwcu punkty zdobyli:
- 3 pkt. – Wojciech Domin III LO Wrocław, Rafał Górzyński I LO Lubin, Laura Stefanowska KLO Legnica,
- 2,5 - Adam Chowanek III LO Wałbrzych, Bartosz Kaczor I LO Głogów, Michał Plata III LO Wrocław, Mikołaj Popek VIII LO Poznań, Cezary Rębiś ZSE Radom, Igor Wojtun I LO Głogów;
- 2 - Anna Cichowska II LO Lubin,
- 1,5 – Michał Węgrzyn ALO PWr Wrocław,
- 1 – Filip Derejski I LO Kraków, Jakub Kutyła ZS Głogów.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech x będzie szukaną największą liczbą zamalowanych kwadratów. Dla n parzystego x ≥ n2/2 (zakolorowana połowa wszystkich pól szachownicy), a dla nieparzystego x ≥ n(n–1)/2+n = n(n+1)/2 (zakolorowana połowa pól szachownicy n × n–1 i jeszcze jedna kolumna). Pokazują to kolorowania przedstawione na rysunkach, które spełniają warunki zadania.
Z drugiej strony dla n parzystego cały kwadrat jest sumą n2/4 rozłącznych kwadratów 2x2, a jeśli w każdym z nich co najwyżej 2 pola są czarne, to x ≤ 2·n2/4 = n2/2. Dla n nieparzystego wiadomo już, że szachownica rozmiaru n–1 × n–1 (czyli parzystego) zawarta w wyjściowej ma maksymalnie połowę pól pokolorowanych, czyli (n–1)2/2. Trzeba teraz pokolorowac resztę pól (Powiedzmy, że została ostatnia prawa kolumna i ostatni dolny wiersz} tak, aby maksymalnie dużo z nich było czarnych. Ostatnią kolumnę kolorujemy całą (co daje dodatkowe n pól). Można to zrobić, bo wiadomo, że istnieje maksymalne kolorowanie szachownicy n–1 × n–1, w którym ostatnia kolumna jest niepokolorowana. Pozostaje ustalenie, ile pól maksymalnie można pokolorować w ostatnim wierszu, liczącym n–1 pól. Kwadrat 2×2 leżący w prawym dolnym rogu szachownicy n×n ma już 2 pola pokolorowane, więc pozostałe 2 muszą zostać białe. Przesuwajac ten kwadrat o jedno pole w lewo, mamy kolejny kwadrat 2×2, który ma 2 pola białe, więc pozostałe 2 muszą być pokolorowane itd. W ten sposob w ostatnim wierszu szachownicy n×n pokolorujemy co drugie pole. Na całej szachownicy pokolorowanych pól będzie nie większa niż (n–1)2/2+n+(n–1)/2 = (n2+n)2 = n(n+1)/2.
Zad. 2. Funkcja liniowa ma postać f(x) = cx + d, zachodzi więc f(a+b) + f(a–b) = c(a+b)+d + c(a–b)+d = ca+cb+d + ca–cb+d = 2ca+2d = 2(ca+d) = 2f(a), ckd.
Zad. 3. Cięciwa BC jest równoległa do prostej l, a promień OA jest do stycznej prostopadły, zatem jest też prostopadły do cięciwy BC. Z twierdzenia Pitagorasa w trójkącie ABD otrzymujemy |BD| = 8√2. Niech |OB| = |OA| = r. Wtedy |OD| = r–4. Z twierdzenia Pitagorasa w trójkącie ODB otrzymujemy r2 = (r–4)2+128, czyli r = 18. Obliczamy pola: PBOC = 16√2·14/2 = 112√2 i POBAC = 16√2·18/2 = 144√2. Stosunek pól wynosi PBOC/POBAC = 7/9.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
